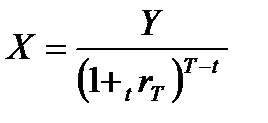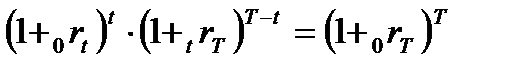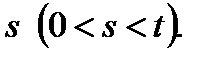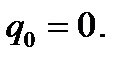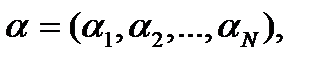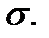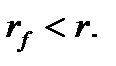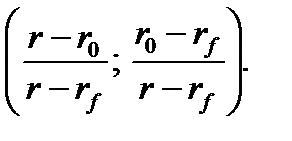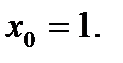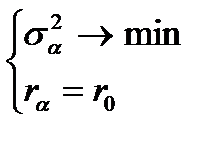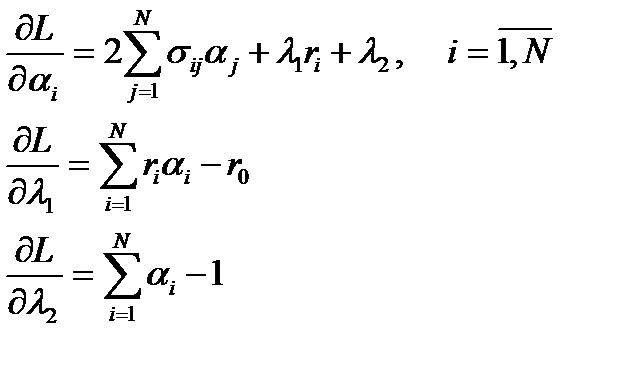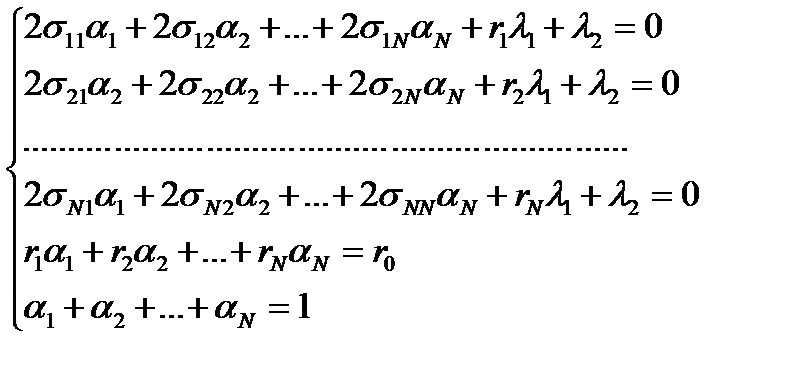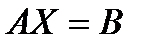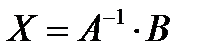Временная структура процентных ставок
В настоящей главе рассматриваются кривая доходности процентных инструментов и теории временной структуры процентных ставок.
Вначале мы остановимся на определении кривой доходности, кривой доходности спот, выведем формулу для расчета теоретической ставки спот. После этого дадим определение форвардной процентной ставки и найдем формулу для ее вычисления. Далее представим три теории временной структуры процентных ставок, а именно, теории чистых ожиданий, предпочтения ликвидности и сегментации рынка.
В один и тот же момент на рынке обращаются облигации, до погашения которых остается различное время. Поэтому можно построить график зависимости доходности бумаг от срока, остающегося до погашения. Для этой цели используют облигации, с одинаковыми характеристиками, например, относящимися к одному классу риска. По оси ординат откладывается уровень процентной ставки, по оси абсцисс — время до погашения. Исходя из конъюнктуры рынка, кривая доходности, ее также именуют временной структурой процентных ставок, может иметь различную форму, как представлено на рис. 3-6.
На рис. 3 кривая доходности параллельна оси абсцисс. Это означает, что процентная ставка одинакова для облигаций с различными сроками погашения. Рис. 4 показывает: процентная ставка возрастает по мере увеличения срока обращения облигаций. Данная форма кривой наиболее характерной для рынка. На рис. 5 представлена обратная ситуация. Рис. 6 описывает конъюнктуру, когда среднесрочные ставки по облигациям выше краткосрочных и долгосрочных. Построив кривую доходности, аналитик получает картину распределения процентных ставок во времени.
Для анализа ситуации на рынке большую роль играет кривая доходности, построенная на основе облигаций с нулевым купоном. Она представляет собой зависимость между доходностью и временем до погашения бескупонных облигаций. Аналитик использует ее для определения возможности совершения арбитражной операции. Любую купонную облигацию можно представить как совокупность облигаций с нулевым купоном, номинал которых равен купону и нарицательной стоимости облигации (для последнего платежа) и выпущенных на сроки, соответствующие срокам погашения купонов и облигации. Доходность купонной облигации и облигаций с нулевым купоном должна быть одинакова, в противном случае возникнет возможность совершить арбитражную операцию. Например, если доходность облигаций с нулевым купоном ниже, чем купонной облигации, то инвестор купит купонную облигацию и продаст пакет облигаций с нулевым купоном, платежи по которым будут соответствовать по размеру и времени платежам по купонной облигации. По данной операции вкладчик получит прибыль, поскольку пакет дисконтных облигаций стоит больше, чем купонная облигация. Если купонная облигация имеет более низкую доходность, чем соответствующая ей дисконтная облигация, то инвестор купит облигации с нулевым купоном таким образом и на такие суммы, чтобы их погашение соответствовало погашению купонов и номинала для купонных облигаций, и продаст созданную им искусственным образом купонную облигацию. Поскольку в этом случае купонная облигация стоит дороже приобретенного вкладчиком пакета облигаций с нулевым купоном, то он получит прибыль.
Различают спотовую процентную ставку и форвардную ставку. Спотовая ставка для периода в п лет — это ставка для облигации с нулевым купоном, до погашения которой остается п лет. Например, эмитируется дисконтная облигация на 1 год с доходностью 10%. Это означает, что ставка спот на один год равна 10%. Выпускается облигация на 2 года с доходностью 11%. Это означает, что спотовая процентная ставка на два года равна 11% и т. д. График зависимости между енотовыми ставками и временем до погашения облигации, называется кривой доходности спот.
Располагая данными о ставках спот за п периодов начисления процента и цене купонной облигации за период п + 1, можно рассчитать теоретическую ставку спот для периода п + 1.
Ставка спот на один год составляет 10%, на два — 11%; купонная облигация, до погашения которой остается три года, продается по цене 916 руб.; номинал облигации — 1000 руб.; купон 8% и выплачивается один раз в год. Необходимо определить теоретическую ставку спот для трех лет.
Как было отмечено выше, доходность купонной облигации и пакета дисконтных облигаций должны быть равны, чтобы исключить возможность арбитражных операций. Поэтому должно выполняться следующее равенство
где: r — теоретическая ставка спот для трех лет.
Решая уравнение, получаем, что r = 11, 5%. Аналогичным образом определяется теоретическая ставка спот для каждого следующего периода. Запишем использованное уравнение в общем виде:

Р— цена купонной облигации;
N— номинал купонной облигации;
r1, r2. rn-1 — известные ставки спот для соответствующих периодов;
rn — ставка спот, величину которой требуется рассчитать.
Допустим, что в приведенном выше примере фактическая трехлетняя ставка спот на рынке равна 11%. Тогда инвестор может купить купонную облигацию за 916 руб. и выпустить три дисконтных облигации (или векселя) с номиналами 80 руб., 80 руб., и 1080 руб., и сроками погашения соответственно через один, два и три года. Пакет дисконтных облигаций стоит 927, 35 руб. Поэтому прибыль вкладчика с одной облигации равна:
927,35-916 =11,35 руб.
Если фактическая трехмесячная ставка спот составляет 13%, инвестор купит дисконтные облигации с номиналами 80 руб., 80 руб., и 1080 руб. и сроками погашения соответственно через один, два и три года за 886, 15 руб., эмитирует на ее основе купонную облигацию (или пакет процентных векселей) и продаст ее за 916 руб. Его доход составит:
916-886,15 = 29,85 руб.
Форвардная процентная ставка — это ставка для периода времени в будущем. Она определяется ставкой спот.
Ставка спот на один год составляет 10%, на два — 11%. Определить форвардную ставку для второго года, т. е. ставку спот, которая будет на рынке через год для облигации с нулевым купоном, выпущенной на год.
Допустим, вкладчик покупает облигацию с нулевым купоном, эмитированную на два года с номиналом 1000 руб. Тогда он платит за нее:
1000(1,11)2 = 811,62 руб.
Инвестор может выбрать иную стратегию, а именно, купить годичную облигацию и после ее погашения реинвестировать средства еще на год. Ему безразлично, какую стратегию выбрать, если во втором случае он также получит через два года 1000 руб., инвестировав сегодня 811, 62 руб. Чтобы ответить на вопрос, под какой процент ему следует реинвестировать средства на второй год, составим уравнение:
Запишем уравнение определения форвардной ставки в общей форме:

rп — ставка спот для периода п;
rn-1 — ставка спот для периода п — 1.
Между доходностью купонной облигации, бескупонной облигации и форвардной ставкой существуют соотношения, которые представлены на рис. 7 и рис. 8.
Источник
Временная структура процентных ставок
Кривая доходности показывает зависимость доходности облигации к погашению от срока ее погашения. Можно построить график зависимости доходности 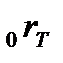
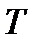
| Рис.5.1. |
| а) |
| б) |
| в) |
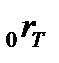 |
Самый простой пример (рис. 5.1 в), когда процентная ставка одинакова для облигаций, имеющих различные сроки погашения. Наиболее характерной ситуацией на рынке облигаций является случай, когда процентная ставка возрастает по мере роста срока погашения и, значит, кривая доходности имеет наклон вверх (рис. 5.1 а). На рынке возможна ситуация, когда доходность по среднесрочным облигациям будет выше, чем по краткосрочным и долгосрочным (рис. 5.1 б).
Обычно на практике временная структура процентных ставок строится по текущим ценам на государственные бескупонные облигации различных сроков погашения, которые принято считать безрисковыми.
Кривая доходности 
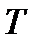
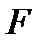
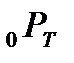
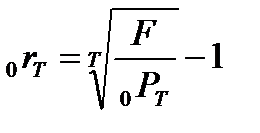
Если мы знаем доходности к погашению к любому моменту времени, то мы можем вычислить приведенную ценность любого платежного потока. Допустим, что нам задан платежный поток в виде поступлений размером 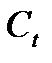
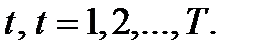
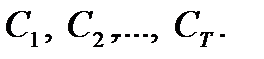
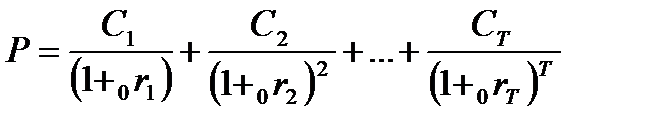
Заметим, что любую купонную облигацию можно представить в виде портфеля бескупонных облигаций, номинал которых равен купону и номинальной стоимости облигации для последнего платежа. Тогда из (5.6) найдем текущую стоимость купонной облигации:
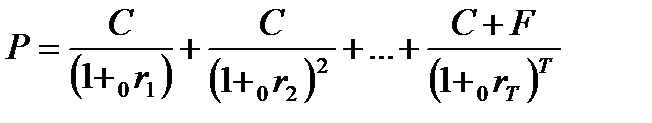
Если процентные ставки 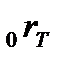
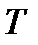
Пример 5.3.Определим текущую рыночную цену  купонной облигации номинальной стоимости купонной облигации номинальной стоимости 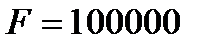 рублей, сроком погашения через 3 года и купоном 7% годовых при условии, что известна кривая доходности на ближайшие три года: рублей, сроком погашения через 3 года и купоном 7% годовых при условии, что известна кривая доходности на ближайшие три года: 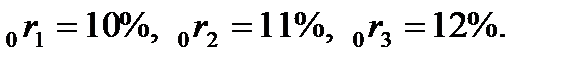 Из (5.7) находим Из (5.7) находим  рублей. рублей. |
Пусть нам известна кривая доходностей 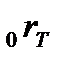

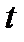
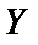
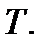
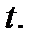
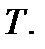
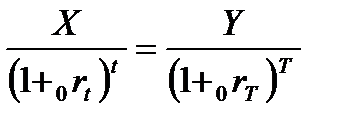
Эквивалентность долгов можно трактовать по-другому. В момент времени 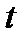
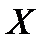
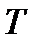
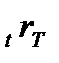
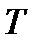
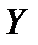
Из двух последних соотношений следует:
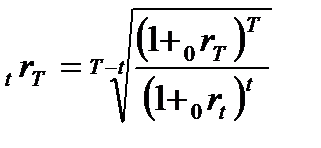
Величина 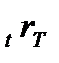

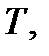
Пример 5.4.Известны доходности облигаций со сроком погашения 2 и 3 года: 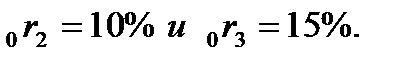 Определим форвардную процентную ставку Определим форвардную процентную ставку 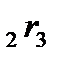 . . 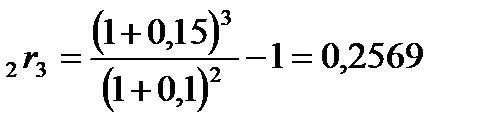 Форвардная процентная ставка между вторым и третьим годом, вычисленная сегодня, равна 25,69%. Форвардная процентная ставка между вторым и третьим годом, вычисленная сегодня, равна 25,69%. |
Временная структура процентных ставок позволяет вычислять форвардные процентные ставки, которые являются прогнозом доходности в будущем.
Рассмотрим пример, как влияет изменение форвардных процентных ставок на инвестиционные проекты. Пусть имеется два инвестора, каждому из которых требуется определенная сумма денег 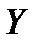
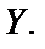
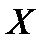
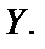
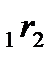
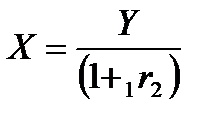
Прошел год. Пусть теперь 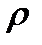

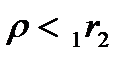

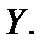
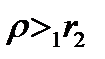
Риск портфеля облигаций
Один из способов снижения рисков, связанных с изменением процентных ставок, основан на изменении дюрации портфеля облигаций. Имеющийся портфель облигаций можно считать платежным потоком, состоящим из купонных и погасительных выплат. Для этого потока можно рассчитать дюрацию – средневзвешенное время выплат.
Дюрация характеризует чувствительность цены портфеля облигаций к изменению доходности. Это означает, что чем больше дюрация, тем большие потери могут быть при изменении доходности, а значит, тем более рискованным является портфель облигаций. Таким образом, инвестор может управлять риском, снижая дюрацию портфеля облигаций.
Дюрация бескупонной облигации равна времени погашения. Для купонной облигации она всегда меньше времени своего погашения. Чем больше купонный процент, тем больший вес имеют купонные платежи по сравнению с номинальной стоимостью, а значит, тем меньше дюрация.
На основе этих рассуждений построена теория предпочтения ликвидности облигаций. Эта теория предполагает, что инвесторы предпочитают краткосрочные бумаги долгосрочным, поскольку у них меньше риск. Так как краткосрочные облигации являются более привлекательными для участников финансового рынка, они обладают более высокой скоростью конвертации в наличные деньги (ликвидностью). Поэтому инвесторы готовы платить за них дополнительную сумму денег, которая называется премией за ликвидность. В результате доходность краткосрочных бумаг будет ниже, чем долгосрочных. В свою очередь, долгосрочные облигации должны предлагать инвесторам более высокую доходность, чтобы они согласились их приобрести. Это означает, что инвестор получит больший доход, если приобретет долгосрочную бумагу вместо последовательного приобретения краткосрочных бумаг в течение того же периода времени.
Форвардные контракты
Форвардный контракт – это согласие между двумя сторонами о будущей поставке актива, которое заключается вне биржи и посредников. В момент заключения контракта оговаривается время исполнения и цена поставки. Под активами понимаются товары, валюта, ценные бумаги и т.д. Продавец актива открывает короткую позицию или продает форвардный контракт. Покупатель активов открывает длинную позицию или покупает форвардный контракт. Само заключение контракта не требует от контрагентов каких-либо расходов.
Как правило, форвардный контракт заключается с целью реальной продажи или покупки актива в будущем. При этом обе стороны хотят обезопасить себя от неблагоприятного изменения цены актива — хеджирование. Контракт может заключаться и с целью спекулятивной игры на разнице цен активов. В этом случае лицо, открывающее длинную позицию, надеется на дальнейший рост цены актива, а лицо, занимающее короткую позицию, рассчитывает на ее понижение.
Цена поставки является результатом согласования позиций контрагентов. Если через некоторое время заключается новый форвардный контракт, то в нем фиксируется новая цена поставки, которая может отличаться от цены первого контракта, поскольку изменились ожидания инвесторов. Таким образом, для каждого момента времени можно определить форвардную цену на актив – цену поставки, зафиксированную в форвардном контракте, который был заключен в данный момент.
Предположим, что через некоторое время один из участников форвардного контракта решил перепродать свои права и обязательства по нему третьему лицу. Пусть к этому времени на рынке установилась новая форвардная цена. Тогда, в зависимости от существующей на момент продажи форвардной цены, короткая и длинная позиции по контракту будут иметь некоторую цену, то есть форвардный контракт сам становится товаром. Возникает вопрос: сколько должен стоить форвардный контракт?
Дальнейшие рассуждения независимы от вида актива. Для определенности будем считать, что актив – бескупонная облигация с номинальной стоимостью 
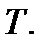


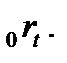
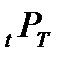

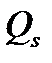

Заметим, что в момент заключения контракта цена поставки равна форвардной цене контракта 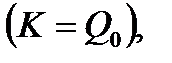
Пусть 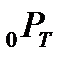
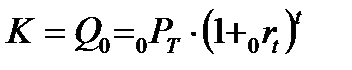
Рассмотрим теперь произвольный момент времени 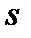
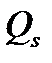
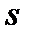
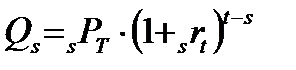
Цена форвардного контракта в момент времени 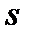
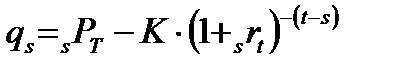
Так как 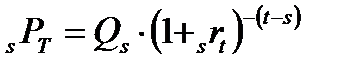
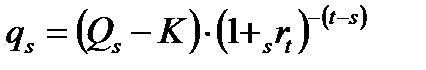
Цена форвардного контракта равна нулю 
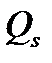
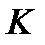
Очевидно, что форвардные цены во многом зависят от временной структуры процентных ставок. Для облигаций, как правило, они растут. То есть 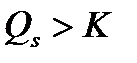
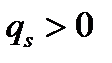

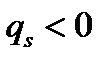
Пример 5.5.Заключен форвардный контракт на поставку бескупонной облигации номинальной стоимостью 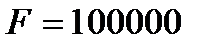 рублей и сроком погашения через рублей и сроком погашения через  лет. По условию контракта его продавец обязан продать облигацию по цене поставки лет. По условию контракта его продавец обязан продать облигацию по цене поставки 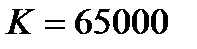 рублей через рублей через 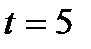 лет. Вычислим форвардную цену лет. Вычислим форвардную цену 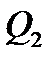 облигации и цену на форвардный контракт облигации и цену на форвардный контракт  через через 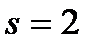 года. Известны форвардные процентные ставки года. Известны форвардные процентные ставки  . Тогда цена облигации через 2 года равна . Тогда цена облигации через 2 года равна  рублей. Форвардная цена контракта рублей. Форвардная цена контракта 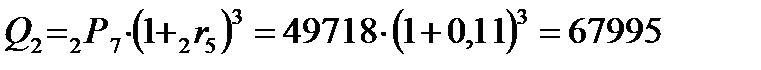 рублей. Значит текущая цена контракта рублей. Значит текущая цена контракта 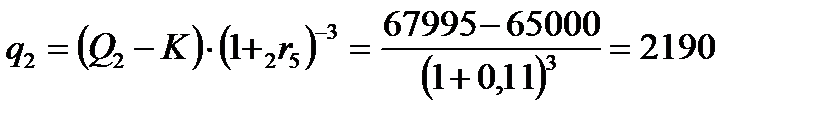 рублей. рублей. |
Глава 6. АКЦИИ
Основные понятия
Одной из наиболее распространенных форм финансирования является продажа части своих активов путем выпуска долевых ценных бумаг. Такие ценные бумаги называются акциями, а компания их выпустившая – акционерным обществом.
Существуют закрытые акционерные общества (ЗАО), акции которых распределяются среди их учредителей, и открытые акционерные общества (ОАО), акции которых продаются и покупаются свободно. Совладельцем ОАО может стать любой, кто приобрел хотя бы одну акцию. Высшим органом управления акционерного общества является собрание акционеров, на котором каждый акционер обладает правом голоса пропорционально сумме имеющихся у него акций. На общем собрании выбирают правление или совет директоров, руководящий текущими делами акционерного общества.
Существуют два основных вида акций, различающихся по выплате дивидендов по ним и степени риска вложения капитала в них. Это обыкновенная акция (ОА)и привилегированная акция (ПА).
ПА определяют фиксированный доход (дивиденды), который должен выплачиваться через равные промежутки времени, чем напоминают купонные облигации. Но они не имеют определенного срока погашения, поскольку могут быть выкуплены эмитентом в любое удобное для него время.
ПА получили свое название в силу того, что в случае ликвидации фирмы претензии владельца ПА удовлетворяются после претензий кредиторов, но раньше, чем обязательства компании перед владельцами ОА. При этом обязательства перед владельцами ПА удовлетворяются не более, чем на сумму номинальной стоимости акций.
Хотя оговорено, что ПА приносит инвестору некий фиксированный дивиденд, в действительности совет директоров имеет право принять решение не выплачивать дивиденды по ПА. Таким образом, хотя ПА близки к облигациям, инвестиции в них являются более рискованными.
Обычно владельцы ПА не имеют права голоса на общем собрании акционеров, в том числе при избрании членов правления. Исключение составляет случай, когда компания в течение определенного периода не выплачивает дивиденды по ПА. В этом случае владельцы ПА имеют право выбрать в правление определенное число директоров.
Обладатели ОА, или просто акционеры компании, являются ее владельцами. Поэтому они полностью принимают риски, связанные с владением капитала данной компании, а в случае ее ликвидации их претензии погашаются в последнюю очередь. С другой стороны, их возможные доходы ничем не ограничиваются. Дивиденды на ОА являются распределением прибыли компании среди ее владельцев. Так как обладатели ОА являются владельцами компании, они имеют право голоса при избрании правления и тем самым имеют возможность влиять на экономическую политику и практическую деятельность компании.
Многих инвесторов покупка акций привлекает не дивидендами, а возможностью получать доход на колебаниях цен акций, покупая их по низкой цене, перед тем как большинство участников фондового рынка начнет это делать, и продавая по высокой цене, перед тем как другие будут это делать.
Прибыль, полученная любой фирмой, неизбежно сопряжена с риском. Поэтому рыночная цена акции данной фирмы во многом будет зависеть от рискованности ее будущих доходов, от отношения акционеров к риску и от уровня процентных ставок по безрисковым ценным бумагам. В условиях неопределенности ее оценка может быть основана только на построении вероятностных моделей.
Портфель инвестиций
Рассмотрим модель инвестирования капитала на единицу времени в экономику, состоящую из 
Обозначим 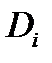
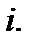
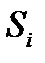
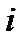
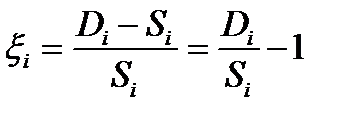
Так как это случайная величина, то используют ее математическое ожидание 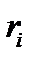
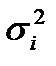
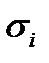
Таким образом, каждой акции 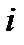
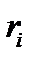


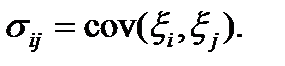
Рассмотрим теперь некоторого инвестора, имеющего капитал 

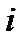
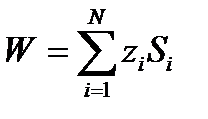
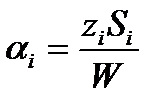
долю инвестиций в акции типа 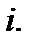
удовлетворяющих условию 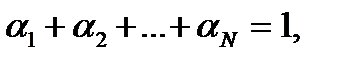
Доходность портфеля инвестиций будет складываться из доходностей отдельных акций. Доходность портфеля инвестиций и его дисперсия определяются по формулам:
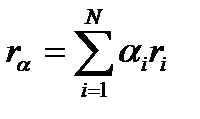
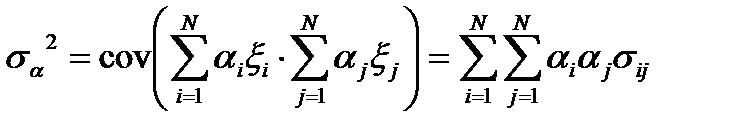
Для каждого допустимого портфеля на плоскости “риск-доходность” можно отметить точки, координаты которых равны среднему квадратическому отклонению и ожидаемой доходности портфеля.
Рисунок 6.1 показывает возможные соотношения между риском и доходностью на данном рынке. Каждая точка области соответствует портфелю инвестиций. Если инвестор заинтересован в максимизации ожидаемой доходности 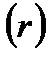
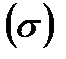
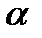
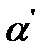
 |
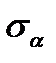 |
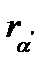 |
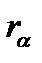 |
| в |
 |
 |
Для каждого допустимого значения доходности 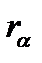
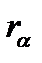
Понятно, что для инвестора координаты граничных точек и соответствующие им портфели являются наиболее важными с точки зрения оптимального выбора инвестиций, так как с учетом правила левого верхнего угла для любой внутренней точки области всегда найдется более предпочтительная точка на границе. Граница области выпукла влево, ее форма показана на рис. 6.1.
Модель оптимизации портфеля
Допустим, что у нас имеется две возможности инвестирования. Первая – в безрисковый актив с доходностью 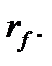
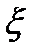
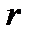
Портфель однозначно будет определяться долей 
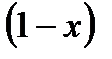
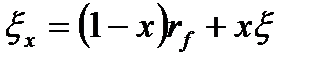
Тогда ожидаемая доходность и среднее квадратическое отклонение доходности портфеля равны
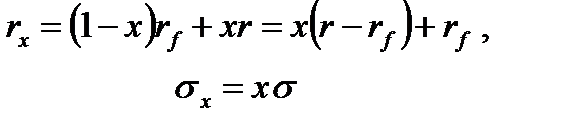
Перед каждым инвестором стоит задача выбора оптимального портфеля по каким-то собственным критериям. Оптимальный портфель определяется конкретным значением 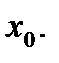
1. Максимум ожидаемой доходности. Предположим, что инвестор не интересуется риском и оптимизирует портфель, стараясь получать максимум ожидаемой доходности. Тогда задача формулируется так:

Решение зависит от знака коэффициента 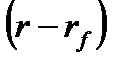
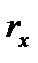
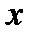
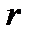 |
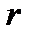 |
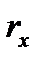 |
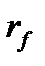 |
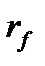 |
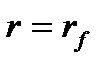 |
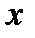 |
| Рис. 6.2. |
| а) |
| б) |
| в) |
В случае а), когда 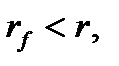
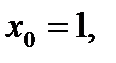
В случае б) 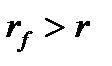
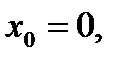
Случай в), когда 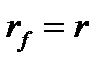
Следует заметить, что второй третий случаи являются очевидными с точки зрения инвестора – он предпочтет безрисковый актив 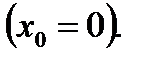
2. Задача Марковица. Допустим, что задан некоторый уровень доходности 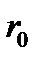
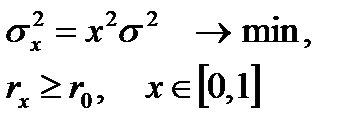
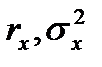 |
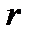 |
 |
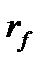 |
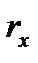 |
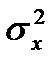 |
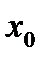 |
1  |
| Рис. 6.3. |
Очевидно, что 
Составляем пропорцию 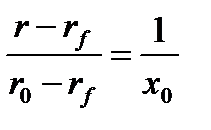
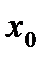
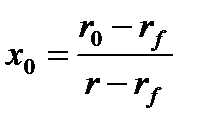
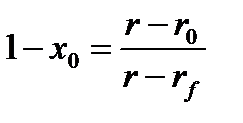
Таким образом, оптимальный портфель в задаче Марковица в простейшем случае безрискового и рискового активов определяется следующей парой:
3. Соотношение “риск-доходность”. Предположим, что предпочтение инвестора определяется минимизацией некоторой функции, связывающей риск и доходность портфеля. Введем функцию рискованности, например, следующим образом:
Коэффициент 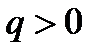
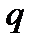
После подстановки из (6.7), задача оптимизации портфеля имеет следующий формальный вид:
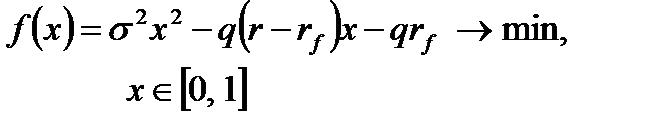
Функция 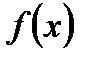
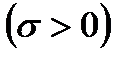
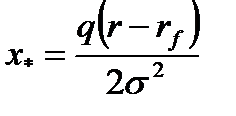
Рассмотрим два варианта выбора оптимального портфеля.
1) 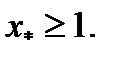
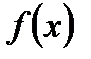
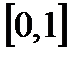
Очевидно, что неравенство 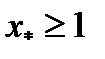
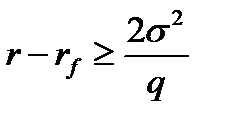
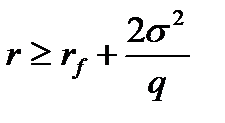
2) Если это неравенство не выполнено и имеет место соотношение
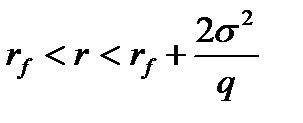
то 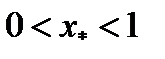
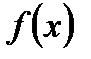
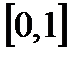
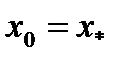
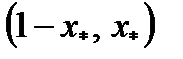

В этом случае ожидаемая доходность и среднее квадратическое отклонение оптимального портфеля равны
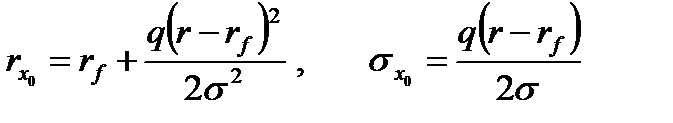
Заметим, что 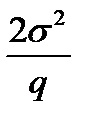

Пример 6.1.Необходимо оптимизировать портфель, состоящий из рискового и безрискового активов. Доходность безрискового актива 12%, то есть 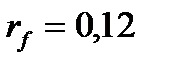 , а доходность и СКО рискового актива равны , а доходность и СКО рискового актива равны  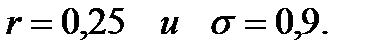 1. Максимум ожидаемой доходности. Оптимальный портфель состоит из инвестиций только в рисковый актив: (0, 1). 2. Задача Марковица. Допустим инвестор согласен на ожидаемую доходность 1. Максимум ожидаемой доходности. Оптимальный портфель состоит из инвестиций только в рисковый актив: (0, 1). 2. Задача Марковица. Допустим инвестор согласен на ожидаемую доходность 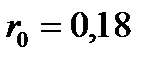 , но при этом хотел бы минимизировать риск. , но при этом хотел бы минимизировать риск. 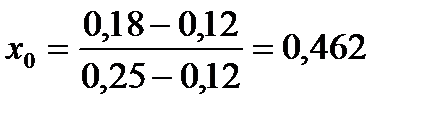 , следовательно, оптимальный портфель (0,538; 0,462). 3. Соотношение “риск-доходность”. Пусть , следовательно, оптимальный портфель (0,538; 0,462). 3. Соотношение “риск-доходность”. Пусть 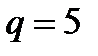 . Тогда . Тогда 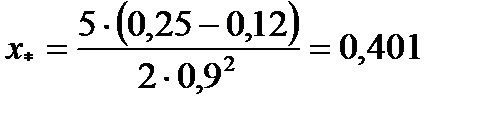 . Оптимальный портфель (0,599; 0,401). . Оптимальный портфель (0,599; 0,401). |
Задача Марковица
Рассмотрим модель инвестирования в 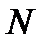
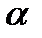

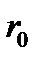
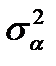
Воспользовавшись формулами (6.4), (6.5) запишем задачу Марковица:
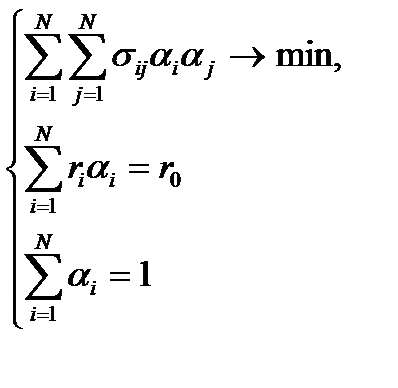
Это задача оптимизации с нелинейной целевой функцией и ограничениями. Для ее решения можно использовать различные методы. Будем искать решение используя метод неопределенных множителей Лагранжа. Целевая функция
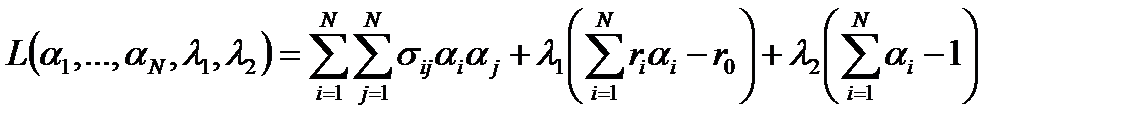
В точке экстремума производные равны нулю:

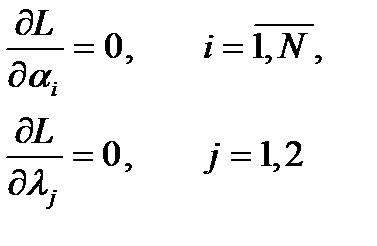
Найдем эти частные производные:
Приравниваем производные нулю:
В матричной форме записи
А- симметричная матрица 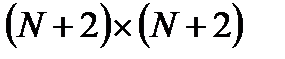

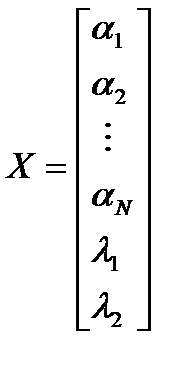
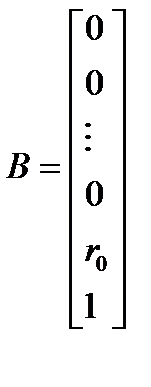
Решая систему уравнений в матричном виде получаем решение:
Так как в векторе 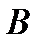




Изменяя значения желаемой доходности, мы всегда получаем оптимальный портфель, а вместе с ним и минимальное СКО, ему соответствующее. Таким образом, это позволяет нам построить границу области допустимых точек на плоскости “риск-доходность”.
Источник