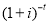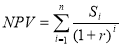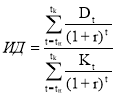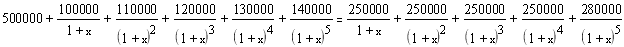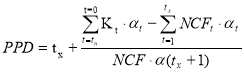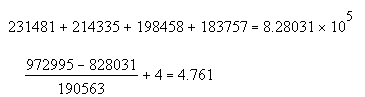Решить задачу определить доходность этой инвестиции

Решение задачи 46

Вам также может быть интересно.

Прежде чем решать задачу необходимо дать уточнение:

— под доходами обычно подразумевается выручка предприятия (в соответствии с законодательством посвященном бухучету и т.д.);

— в задаче под ежемесячными доходами должен подразумеваться дополнительный доход, т.е. доход минус издержки равняется дополнительный доход. В противном случае оценить эффективность нельзя!

— либо следует воспользоваться следующей трактовкой: Сравнивая между собой приведенные величины денежных притоков и оттоков по финансовой операции, определяют важнейший финансовый показатель чистая приведенная стоимость (NPV – от английского net present value ). Наиболее общая формула определения этого показателя:

,

где I₀ – первоначальные инвестиции в проект (оттоки денег),

PV – приведенная стоимость будущих денежных потоков по проекту.

При использовании этой формулы все денежные притоки (доходы) обозначаются положительными цифрами, оттоки денежных средств (инвестиции, затраты) – отрицательными.

Тогда под ежемесячными доходами «.. за первые пять месяцев составят соответственно: 20; 40; 50; 80 и 100 млн. руб.» — понимается «приведенная стоимость будущих денежных потоков по проекту»

Для того чтобы инвестиционное решение проекта было эффективным, т.е. выгодным с коммерческой точки зрения, необходимо, чтобы денежные оттоки, связанные с ним (инвестиции, текущие затраты), как минимум, компенсировались денежными притоками. Однако, учитывая принцип временной стоимости денег, т. е. тот факт, что разновременные денежные потоки имеют неодинаковое значение, требуется сначала привести их к одному моменту времени.

Следовательно, чтобы оценить инвестиционное решение в задаче, следует:

• рассчитать и приурочить к соответствующим моментам (интервалам) времени все денежные потоки, которые генерирует данное решение;

• привести эти потоки по ставке, соответствующей их риску, к одному моменту времени (моменту оценки);

• просуммировать полученные приведенные денежные потоки с учетом их знака (притоки — со знаком “плюс”, оттоки — со знаком “минус”). Полученная в результате величина называется чистой приведенной стоимостью (чистым приведенным доходом) NPV.

Таким образом, NPV — это сумма денежных потоков, связанных с данным инвестиционным решением, приведенная по фактору времени к моменту оценки, т.е.

NPV = — CF₀ + + + …. +… +

где С Fj — денежный поток, приуроченный к j-му моменту (интервалу) времени;

n — срок жизни проекта.

Срок операции n в общем случае измеряется в годах. Если же реальная операция не отвечает этим условиям, т.е. интервалы между платежами не равны году, то в качестве единицы измерения срока принимаются доли года, измеренные как правило в месяцах, деленных на 12.

NPV > О означает следующее:

• выраженный в “сегодняшней” оценке эффект от проекта составляет положительную величину;

• проект имеет доходность более высокую, чем ставка дисконта r , требуемая на рынке капиталов от инвестиций с таким уровнем риска.

Таким образом, данный критерий идеально подходит для оценки отдельных инвестиционных проектов, абсолютной величины их эффекта.

Тогда в цифрах решение задачи:

NPV = — 200 + + + + + + = 78,95 (млн .р уб.)

В качестве ставки дисконта r используется значение из условия задачи 13,5%.

Полученный NPV означает следующее:

а) ожидаемый абсолютный эффект от данного проекта составляет 78,95 млн. руб.

б) доходность проекта ожидается на уровне, более высоком, чем 10% годовых в рублях.

Для того чтобы оценить доходность инвестиционного решения в процентах годовых, используется другой критерий, называемый внутренней ставкой (нормой) доходности.

IRR — позитивная ставка доходности инвестиционного проекта. Ставка дисконта при которой NPV = 0.

IRR — это позитивная доходность инвестиционного проекта, рассчитанная по ставке сложного процента с ежегодной капитализацией доходов.

Зная, как интерпретируется показатель NPV легко объяснить, почему IRR определяется как такая ставка дисконта, при которой NPV = 0.

Таким образом, для того чтобы найти IRR необходимо решить уравнение:

0 = — CF₀ + + + …. +… +

Формулы, позволяющей решить такое уравнение, не существует. Поэтому уравнение решается приближенными метода ми, чаще всего с использованием линейной интерполяции, а именно:

а) наугад берутся две ставки дисконта — r₁ и r₂, r₁

б) используя каждую из ставок, рассчитывают два значения показателя NPV (чистого приведенного дохода) — NPV₁ и NPV₂;

в) приближенное значение IRR получают по формуле:

IRR = r₁ + 1 × (r₂ — r₁).

Для получения более точного значения IRR расчеты несколько раз повторяют, сужая интервал между r₁ и r₂.

Отсюда приближенное значение IRR можно определить следующим образом:

IRR = 244,4% годовых.

Индекс прибыльности ( profitability index , PI) показывает относительную прибыльность проекта, или дисконтированную стоимость денежных поступлений от проекта в расчете на единицу вложений. Он рассчитывается путем деления чистых приведенных поступлений от проекта на стоимость первоначальных вложений:

Индекс прибыльности проекта:

PI = 78 ,95 : 200 = 0,39

Учитывая, что NPV = 78,95 (млн .р уб.) > 0, IRR = 244,4% годовых можно сделать вывод – проект эффективен.

Мы дали Вам направление, дальше действуйте, и все у вас получится!

Источник

Решение задач по инвестиционному анализу 2

Ниже приведены условия и решения задач. Закачка решений в формате doc и mcd начнется автоматически через 10 секунд.

Задание №2

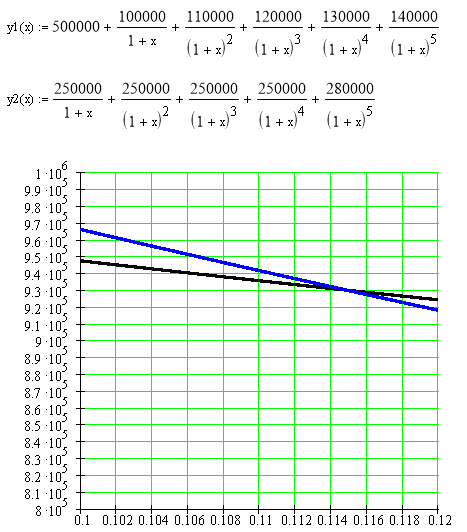
Предприятие собирается приобрести оборудование, чтобы самостоятельно производить детали, которые раньше покупали от поставщиков. Стоимость оборудования — 500000. Эксплуатационные расходы в первый год составляют100000 и ежегодно возрастают на 10000. За поставку деталей ежегодно платили поставщикам по 250000. Срок эксплуатации оборудования – 5 лет. Ликвидационная стоимость – 30000 (чистый доход от продажи оборудования в конце 5-го года). Ставка по альтернативным проектам- 8% годовых. Эффективна ли данная инвестиция ( NPV , PI , IRR , MIRR , PP , PPD )? Дайте письменное заключение о целесообразности реализации проекта.

Дисконтированный поток платежей

Для проекта определяем приведенную стоимость поступлений от инвестиций по формуле:

, где S i – поступления в i -ый период времени, r — норма пр и были альтернативных проектов.

Определим индекс прибыльности.

ИД определим по формуле:

PI = 1018595/972995 = 1,047

Внутренняя норма доходности ( IRR ) – это такая норма дисконта, при которой сумма дисконтированных доходов за жизненный цикл проекта равна сумме дисконтированных инвестиций.

Определим внутреннюю норму доходности для каждого из проектов.

Для первого проекта решим уравнение:

∑ CF k / ( 1 + IRR ) k = ∑ INV t / (1 + IRR) t

Решим уравнение аналитически, методом подбора.

Следовательно, IRR = 0, 115 .

Опр еделим срок окупаемости для проекта с учетом дисконтирования .

При ставке сравнения 8% имеет смысл инвестировать средства в данный проект, имеем положительный чистый дисконтированный доход , индекс доходности 104,7%. Однако при увеличении инфляции свыше 11 ,5 % не имеет смысла инвестировать средства в данный проект ( IRR =0,115), так же срок окупаемости проекта достаточно высокий и составляет 4,761 года, и близок к эксплуатационному сроку работы оборудования.

Фирма «Смирнов и Андрианов» покупает завод по производству глиняной посуды за 100 млн.рублей. Кроме того расчёты показывают, что для модернизации этого предприятия в первый же год потребуются дополнительные затраты в 50 млн. рублей. Однако, при этом предполагается, что в последующие 9 лет этот завод будет обеспечивать ежегодные денежные поступления по 25 млн. рублей. Затем, через 10 лет, предполагается, что фирма продаст завод по остаточной стоимости, которая составит согласно расчётам 80 млн. рублей. Средняя ставка доходности 10% . Эффективна ли данная инвестиция ( NPV , PI , IRR , MIRR , PP , PPD )? Дайте письменное заключение о целесообразности реализации проекта

Источник

Тема 3. Управление инвестициями

Цель практикума по данной теме — сформировать навык решения задач по оценке эффективности, риска инвестиционных проектов, по формированию бюджета и выбору источников финансирования капитальных вложений.

Методические указания

Приступая к рассмотрению примеров и самостоятельному решению задач, необходимо внимательно прочесть контент по соответствующему вопросу темы. Базовые концепции в данной теме — это концепция денежного потока, концепция временной ценности денег, концепция компромисса между риском и доходностью, концепция альтернативных затрат. Важнейшие понятия: чистый дисконтированный доход ­ ЧДД (Net Present Value — NРV), внутренняя норма доходности — ВНД (Internal Rate of Return — IRR), индекс доходности (рентабельности) инвестиции (Profitability Index — РI). Эти понятия следует выучить и разобраться в их соотношениях.

В решении задач используются формулы, объяснение которых представлено в контенте. Для облегчения поиска необходимых разъяснений в контенте нумерация формул и обозначения в практикуме такие же, как и в контенте.

3.1. Оценка эффективности и риска инвестиционных проектов

В данном параграфе используются следующие обозначения:

A — одинаковый ежегодный (ежеквартальный, ежегодный ) приток/отток денег (доходы, расходы, разность доходов и расходов), ден. ед.;

ARR — коэффициент эффективности инвестиций;

— приток (отток) — разность доходов и расходов (текущих и капитальных) в t-й период (), ден. ед.;

d — доходность (эффективность, рентабельность), %;

D — общий доход от проекта (учетная оценка), ден. ед.;

D РР — дисконтированный срок окупаемости, периоды (годы);

— доход от инвестиционного проекта (разность между текущими доходами и текущими расходами) в t-ом периоде, ден. ед.;

D_ср — среднегодовой доход, ден. ед.;

FV — будущая (наращенная) стоимость денежного потока, ден. ед.;

I — стоимость эксплуатируемых инвестиций (среднегодовая), ден. ед.;

IRR — внутренняя норма доходности (рентабельности), %;

K — объем капиталовложений (инвестиции), ден. ед.;

К_ост — непокрытый остаток капиталовложений, ден. ед.;

m — количество периодов (обычно меньше срока эксплуатации проекта);

MIRR — модифицированная внутренняя норма доходности (рентабельности), %;

n — срок реализации инвестиционного проекта, периоды (годы);

NPV — чистый дисконтированный (приведенный) доход, ден. ед.;

Р — прибыль (среднегодовая), ден. ед.;

PI — индекс рентабельности (доходности) инвестиций, %;

РР — срок окупаемости, периоды (годы);

PV — общий дисконтированный (приведенный) доход, ден. ед.;

— общий дисконтированный доход за первые k лет, ден. ед.;

r — процентная ставка (ставка дисконтирования, альтернативные издержки), %;

t — номер периода (года);

WACC — средняя (средневзвешенная) стоимость капитала;

Задача 3.1.1.

В рассмотрении находится инвестиционный проект. Согласно ему инвестор должен вложить 10 тыс. у. е. Обещанный ему среднегодовой доход составляет 3 тыс. у. е. Найти срок окупаемости, выраженный в годах и месяцах.

Методические указания: использовать формулу (3.1.1).

Доход поступает равномерно, поэтому используем следующую формулу:

PP = K/D_ср = 10000/3 тыс. = 3,33 года.

Выразим нецелую часть года в месяцах:

0,33 12 = 4 месяца.

Ответ: Cрок окупаемости инвестиционного проекта — 3 года и 4 месяца.

Задача 3.1.2.

Инвестиционный проект генерирует неравномерный денежный поток (табл. 3.1.1). Найти срок окупаемости проекта.

Таблица 3.1.1 — Денежный поток по проекту, у. е.

Методические указания: использовать формулу (3.1.2).

Считаем сумму доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения:

сумма доходов за первые 3 года составляет

200 + 400 + 400 = 1000 у е. что недостаточно для покрытия инвестиций;

сумма доходов за первые 4 года составляет

200 + 400 + 400 + 600 = 1600 у. е., что покрывает инвестиции с избытком, срок окупаемости, согласно формуле (3.1.2) — 4 года.

Найдем более точно срок окупаемости:

через 3 года непокрытый остаток капиталовложений (К_ост) равен:

который может быть покрыт за 0,83 (500/600) четвертого года, за 10 (0,83 12) месяцев.

Ответ: Срок окупаемости инвестиций 3 года и 10 месяцев.

Задача 3.1.3.

В инвестиционный проект предлагается вложить 1600 у. е. Обещанный среднегодовой доход составляет 400 у. е. Ожидается, что ставка доходности (дисконтирования) не будет меняться и будет составлять 10 % годовых. Найти абсолютный и дисконтированный срок окупаемости.

Методические указания: использовать формулы (3.1.1), () и ().

Абсолютный срок окупаемости находится непосредственно из формулы (3.1.1), поток доходов равномерный:

РР=К/ D_ср = 1600/400 = 4 года.

Для расчета дисконтированного срока окупаемости считаем сумму дисконтированных доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения. Сумма доходов за первые 5 лет составляет:

что меньше суммы капиталовложений.

Сумма доходов за первые 6 лет составляет:

, что покрывает исходную сумму капиталовложений, срок окупаемости — 6 лет.

через 5 лет непокрытый остаток капиталовложений (К_ост) равен:

Кост = K — PV 5 = 1600 — 1516,32 = 83,68 у. е.,

который может быть покрыт за 0,37 (83,68/225,99) шестого года, за 4,4 (0,37 12) месяца.

Ответ: Абсолютный срок окупаемости инвестиций составит 4 года; дисконтированный срок окупаемости — 5 лет и 4,4 месяца.

Задача 3.1.4.

Компания N располагает двумя альтернативными вариантами инвестиционных проектов, требующих одинаковых вложений. Данные, характеризующие эти проекты, приведены в табл. 3.1.2 и на рис. 3.1.1. Найти срок окупаемости инвестиций для каждого из проектов. Выбрать проект для реализации с точки зрения: а) сохранения ликвидности; б) получения дохода; в) эффективности. Принять решение на основе учетных оценок.

Таблица 3.1.2 — Денежные потоки по проектам, А и Б, у. е.

Денежные потоки по проектам

Рис. 3.1.1 — денежные потоки по проектам, А и Б: синим цветом обозначены вложения, коричневым — денежные потоки для проекта А; желтым — денежные потоки для проекта Б.

Методические указания: использовать формулы (3.1.2) и(3.1.3).

1. Решим задачу на основе учетных (не дисконтированных) оценок.

Срок окупаемости проекта, А:

Считаем сумму доходов нарастающим итогом до тех пор, пока она не превысит капиталовложения:

сумма доходов за первые 3 года составляет

150 + 200 + 300 = 650 у. е., что недостаточно для покрытия инвестиций;

сумма доходов за первые 4 года составляет

650 + 400 = 1050 у. е., что покрывает инвестиции с избытком, срок окупаемости, согласно формуле (3.1.2), — 4 года.

Найдем более точно срок окупаемости:

через 3 года непокрытый остаток капиталовложений (К_ост) равен:

который может быть покрыт за 0,875 (350/400) четвертого года, за 10,5 (0,875 12) месяцев.

Таким образом, срок окупаемости проекта, А составляет 3 года и 10,5 месяца.

Аналогичным образом находим срок окупаемости проекта Б — 3 года, а более точно:

К_ост = K — (D₁ + D₂) = 1000 — (500 + 400) = 100 у. е.,

который может быть покрыт за 0,33 (100/300) третьего года, за 4 (0,33 12) месяца.

Таким образом, срок окупаемости проекта Б составляет 2 года и 4 месяца.

Рассчитаем общий доход (D) по проектам:

D_A = 150 + 200 + 300 + 400 + 500 + 600 = 2150 у. е.

D_Б = 500 + 400 + 300 + 100 = 1300 у. е.

Эффективность проекта можно оценить путем расчета коэффициента эффективности инвестиций, для чего необходимо рассчитать среднегодовую прибыль (Р) и среднегодовую стоимость эксплуатируемых инвестиций (I):

Среднегодовая стоимость эксплуатируемых инвестиций у обоих проектов одинаковая:

I = K/2 = 1000/2 = 500 у. е.

Коэффициент эффективности инвестиций:

Ответ: С точки зрения ликвидности (по сроку окупаемости) более предпочтителен проект Б, окупающийся через 2 года и 4 месяца, чем проект, А, окупающийся за 3 года и 10,5 месяца. Однако проект, А приносит больше дохода (2150 у. е.), чем проект Б, (1300 у. е.) Проект, А также более эффективен (), чем проект Б ().

Задача 3.1.5.

Рассматривается вопрос о приобретении одной из двух машин, А и B. Ожидается, что их эксплуатация будет приносить доход в течение и лет соответственно (табл. 3.1.3). Альтернативные издержки равны 10 %. Вычислите чистую приведенную стоимость каждой машины. Какую машину следует купить?

Таблица 3.1.3 — Потоки денежных средств для проектов А и В, руб.

Потоки денежных средств (тыс. р.)

Методические указания: использовать формулу (3.1.6).

Используем стандартную формулу чистой приведенной стоимости:

Исходя из показателя чистой приведенной стоимости, следует выбрать машину В, NPV у этого проекта больше. Однако следует помнить, что критерий NPV используется при сравнении равномасштабных проектов. Здесь проекты имеют разные масштабы как с точки зрения вложений, так и срока эксплуатации. Поэтому необходимо привлечь критерий рентабельности инвестиций — PI:

PI = PV / K = (NPV+K) / K.

PI (A) = (100 + 100) / 100 = 2 = 200 %;

PI (B) = (180 + 120) / 120 = 2,5 = 250 %.

По данному критерию также следует отдать предпочтение проекту В.

Ответ: Следует выбрать машину В.

Задача 3.1.6.

У компании имеются два проекта -А и Б. Каждый проект имеет издержки в 10 тыс. р., альтернативные издержки для каждого проекта составляют 12 %. Ожидаемые денежные потоки, генерируемые этими проектами представлены в таблице 3.1.4.

Таблица 3.1.4 — Денежные потоки по двум проектам, А и Б

а) подсчитать период окупаемости, чистую приведенную стоимость, коэффициент внутренней нормы доходности для каждого проекта;

б) решить, какой проект должен быть принят, если они независимые;

в) решить, какой проект должен быть принят, если они взаимоисключаемые;

г) оценить, как изменение ставки дисконтирования могло бы привести к конфликту в ранжировании этих двух проектов по чистой приведенной стоимости и по внутренней норме доходности;

д) ответить на вопрос, какой проект предпочтительнее — при r = 4,5 % или при r = 8 %?

Методические указания: использовать формулы (3.1.2), (3.1.5), (3.1.6), (), () и ().

а) 1. Расчет периода окупаемости.

Окупаемость проекта, А (лет):

ожидаемый поток доходов меняется из года в год, период окупаемости можно определить, суммируя доходы по годам до тех пор, пока их сумма не станет равной первоначальному вложению. Через 2 года накопленный доход 9,5 тыс. р. (6,5 + 3) меньше капвложений, через 3 года — 12,5 тыс. р. (6,5 + 3 + 3) — больше.

Точный расчет срока окупаемости:

Аналогичный расчет сделаем для проекта Б.

Окупаемость проекта Б (лет):

года.

При независимости оба проекта следует принять, срок окупаемости не превышает срока эксплуатации проектов. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий меньший срок окупаемости.

2. Чистая приведенная стоимость:

При независимости оба проекта следует принять, NPV для обоих проектов положителен. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий больший чистый дисконтированный доход.

3. Внутренняя норма доходности:

Для расчета внутренней нормы доходности воспользуемся приблизительным расчетом на основе формулы:

.

В качестве r₁ используем исходную ставку дисконтирования 12 %. В качестве r₂ возьмем, например, 20 %.

Рассчитаем NPV со ставкой 20 %:

При независимости проекты следует принять, если PI не превышает стоимости привлекаемых средств. Если следует выбрать один, то более предпочтительным оказывается проект, А, имеющий большую внутреннюю норму доходности.

б) По всем рассмотренным критериям оба проекта являются приемлемыми. Таким образом, оба проекта должны быть приняты, если они независимые.

в) При альтернативности проектов выбрать следует проект А. Он лучше по всем показателям.

г) Найдем r, при котором NPV двух проектов равны (точку Фишера):

Домножим обе части уравнения на :

Подставим в левую часть r = 6 % и r = 7 %. В первом случае левая часть уравнения:

Во втором случае:

Теперь возьмем :

.

Поскольку существует точка Фишера, конфликт критериев при выборе инвестиционного проекта возможен.

Если r 0, а при другой NPV d, эффективность проекта выше эффективности предприятия, поэтому проект приемлем.

Теперь рассмотрим критерии, основанные на дисконтированных оценках. Первый — общий дисконтированный доход:

PV Методические указания: 1) Оценить инвестиционный проект по всем возможным критериям с учетом и без учета дисконта денежных потоков; 2) Результаты расчета денежных потоков представить на графиках суммарной величины дисконтируемых и недисконтируемых денежных потоков в зависимости от времени; 3) Использовать формулы (), (), (3.1.1) — ().

3.2. Формирование бюджета капиталовложений

Задача 3.2.1.

Имеются четыре проекта, характеристики которых приведены в табл. 3.2.1.

Таблица 3.2.1 — Денежные потоки по четырем проектам

Ставка дисконтирования r =10 %.

Требуется сформировать бюджет капиталовложений при условии, что предприятие может инвестировать 1600 тыс. р.:

а) проекты поддаются дроблению;

б) проекты не поддаются дроблению.

Методические указания: использовать формулы (3.1.4) — (3.1.6), (3.1.9), (3.2.1) — (3.2.4).

Дано:

D для всех проектов в двух периодах в табл. 3.2.1;

Решение:

Формирование бюджета основывается на расчете значений критериев PV; NPV; PI для всех проектов. Общий дисконтированный доход PV находится по формуле

Чистый дисконтированный доход NPV:

Индекс рентабельности инвестиции PI:

Рассмотрим формирование бюджета при двух условиях:

а) проекты поддаются дроблению.

В данном случае проекты упорядочиваются по убыванию показателя PI: А, Г, В, Б.

В бюджет полностью включаются первые проекты, сумма инвестиций для которых не более имеющейся, 1600 тыс. р.:

Следовательно, полностью будут реализованы проекты А и Г, а проект В может быть реализован частично, доля его реализации определяется по формуле

Читайте также:  Асик s17 pro доходность

Таким образом, оптимальная структура инвестиционного портфеля в случае, когда проекты могут быть реализованы частично, представлена в табл. 3.2.2.

Таблица 3.2.2 — Инвестиционный портфель (проекты поддаются дроблению)

31,4 (92,4 0,333)

б) проекты не поддаются дроблению.

В этом случае оптимальная структура бюджета капиталовложений определяется перебором всех возможных вариантов сочетаний проектов и расчетом суммарного PI для каждого варианта. Комбинация, максимизирующая суммарный PI, будет оптимальной.

Возможны следующие сочетания проектов в портфеле: А + Б, A + В, А + Г, Б + В, В + Г.

Расчет общего индекса рентабельности инвестиций осуществляется по формуле

Максимальный общий индекс рентабельности получается при реализации проектов А и Г.

Рассчитаем суммарный NPV для каждого варианта.

Максимальный суммарный чистый дисконтированный доход также получается при реализации проектов, А и Г (табл. 3.2.3).

Таблица 3.2.3 — Варианты инвестиционных портфелей (проекты не поддаются дроблению)

А + Г

200

575,2

1,411

Ответ: Мы реализуем проекты А и Г, суммарный NPV для них наиболее высок.

Ответ: а) проекты поддаются дроблению, поэтому мы можем реализовать два проекта полностью на 100 % (проекты А и Г), а проект B только на 33,3 %. Суммарный NPV в этом случае равен 606,6 тыс. р.; б) если проекты не поддаются дроблению, то следует реализовать проекты А и Г, при этом суммарный NPV равен 575,2 тыс. р. (PI = 1,411).

Задача 3.2.2.

Имеются четыре проекта, характеристики которых приведены в табл. 3.2.4. Ставка дисконтирования r =10 %.

Таблица 3.2.4 — Денежные потоки по четырем проектам, тыс. р.

Требуется сформировать бюджет капиталовложений при условии, что предприятие может инвестировать в год 2000 тыс. р., а во — 1000 тыс. р.

Методические указания: использовать формулы (3.1.4)-(3.1.6), (3.1.9), (3.2.5).

Дано:

D для всех проектов в двух периодах в табл. 3.2.4;

Решение:

Рассчитываем значение критериев PV; NPV; PI для всех проектов.

Общий дисконтированный доход для любого проекта находится по формуле:

Чистый дисконтированный доход NPV:

Индекс рентабельности инвестиции PI:

Рассчитываем NPV в. случае, если проект откладывается на 1 год:

Рассчитываем индекс потерь в случае, если проект откладывается на 1 год:

Аналогично рассчитываем индексы потерь для других проектов:

Проекты упорядочиваются по убыванию индекса потерь: А, Г, В, Б.

В первый год реализуются проекты с максимальным индексом потерь, для которых достаточно капиталовложений:

Таким образом, в 1-й год реализуем три проекта: А, Г и В.

Ответ: В план 1-го года следует включить проекты, А, Г и В. На 2-й год планируется проект Б.

Задача 3.2.3.

Имеется семь проектов, для которых рассчитаны внутренние нормы доходности (табл. 3.2.5). Для реализации проектов можно привлечь шесть источников, характеризующихся разными ценами (табл. 3.2.6). Требуется составить бюджет капиталовложений.

Таблица 3.2.5 — Внутренняя норма доходности и требуемые инвестиции по проектам

Требуемые инвестиции, тыс. р.

Внутренняя норма доходности, %

Таблица 3.2.6 — Цены и объемы источников финансирования

Методические указания: 1) Использовать формулы из. п. 3.2.3; 2) Ввести дополнительные обозначения: — инвестиции, необходимые для проектов, А,…,Ж; — объем источников финансирования; — цены источников финансирования.

Дано:

— в табл.3.2.5;

IRR — в табл. 3.2.5;

— в табл.3.2.6;

— в табл.3.2.6

Решение:

Прежде всего необходимо упорядочить проекты по убыванию IRR: В, Г, Ж, Д, Б, Е, А.

Затем упорядочиваются источники финансирования по возрастанию цены: И, П, М, К, Л, Н.

Проект В требует 3000 тыс. р. Одного самого дешевого источника И недостаточно. Привлекаем источник П:

(3 000 15), проект Е (и проект А, имеющий еще более низкую внутреннюю норму доходности) в бюджет не включается.

Итоговый бюджет представлен в табл. 3.2.7.

Таблица 3.2.7 — Бюджет капиталовложений

Ответ: В бюджет капиталовложений включаются проекты В, Г, Ж, Д и Б, финансируемые за счет источников И, П, М, К и Л. При этом из источника Л используется только 200 тыс. р.

Задача 3.2.4.

Компания имеет возможность инвестировать ежегодно не более 20 млн р.; кроме того, все доходы от дополнительно введенных инвестиционных проектов также могут использоваться для целей инве­стирования. На момент анализа имеются четыре независимых проекта (табл. 3.2.8).

Таблица 3.2.8 — Денежные потоки по имеющимся проектам

Требуется составить портфель капиталовложений, если стоимость источников финансирования 12 %.

Методические указания: использовать формулы (3.1.4), (3.1.6) и (3.1.9).

Дано:

— в табл. 3.2.8;

= 20 млн р.

Решение:

Прежде чем приступать к составлению портфеля, необходимо рассчитать значения критериев NPV и PI для каждого проекта:

;

Для четвертого проекта рассчитаем NPV на начало 1-го года:

На начало 2-го года (начало эксплуатации проекта D) NPV составит:

Все проекты являются приемлемыми, все они обеспечивают положительный чистый дисконтированный доход.

Индекс рентабельности инвестиций рассчитаем с учетом приведения всех денежных потоков к началу 1-го года (концу 0-го):

Для расчета индекса рентабельности проекта D необходимо рассчитать современную стоимость капиталовложений:

Критерий РI дает возможность ранжировать проекты по степени предпочтительности: С, В, A, D.

В нулевой год имеется 20 млн р., следовательно, можно начать реализацию проектов С и В, для которых требуется 5 и 15 млн р. соответственно. На следующий год у компании будет еще 20 млн р., а также 12 млн р., полученных от эксплуатации проектов С и В (8 + 4), итого 32 млн р., которых оказывается недостаточно для реализации проекта D. При условии, что проекты могут реализоваться только в указанные сроки (не могут начинаться раньше или позже), суммарный чистый дисконтированный доход в рассматриваемом варианте составит:

Рассмотрим другой вариант: реализуем вначале проект, А, для которого требуется 20 млн р. Тогда на следующий год у компании кроме ее ресурсов в 20 млн р. добавится 25 млн р. от эксплуатации проекта, А, всего 45 млн р., что будет достаточно для реализации проекта D. В таком случае суммарный чистый дисконтированный доход составит:

Таким образом, видим, что при данных условиях критерий PI прямо указывает на первый вариант, который в конечном итоге дает меньше чистого дисконтированного дохода.

Однако следует иметь в виду, что в первом варианте остаются неиспользованными 32 млн р., настоящая стоимость которых составляет 28,6 млн р. (32/1,12), что в 2 раза перекрывает доход от реализации проектов А и D.

Ответ: Следует реализовать проекты С и В.

Задача 3.2.5.

В табл. 3.2.9 приведены исходные данные по двум альтернативным проектам. Требуется выбрать один из них при условии, что стоимость капитала, предназначенного для инвестирования проекта: а) 8 %; б) 15 %. Определить точку Фишера.

Таблица 3.2.9 — Денежные потоки по имеющимся проектам, тыс. р.

Источник