Npv внутренний коэффициент окупаемости irr

Инвестиционные показатели NPV, IRR: Excel на службе у финансового директора

Как рассчитать NPV и IRR, оценить эффективность инвестиционных проектов, рассчитать сумму аннуитета и проверить банк на честность. Финансовых формул в Excel много. Часть из них предназначена для расчета амортизации разными способами. Другие – для определения стоимости ценных бумаг. Третьи для чего-то еще. Здесь мы разберем самые главные и «животрепещущие» (на мой взгляд).

Это формулы, которые позволят рассчитать:
— NPV (Net Present Value) — чистую приведенную стоимость.
— IRR (Internal Rate of Return) — внутреннюю ставку доходности.
— Аннуитеты – равномерные платежи.

Также рассмотрим некоторые нюансы использования этих формул. Все расчеты можно найти в приложенном файле. Основной акцент сделан на функции Excel, поэтому саму финансовую математику разбирать особо не будем.

Оценка целесообразности проекта с помощью NPV

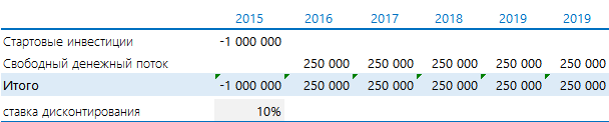
Есть проект, который ежегодно в течении 5 лет будет приносить 250 000 руб. Нужно потратить 1 000 000 руб. Предположим, что ставка дисконтирования равна 10%.

Оцениваем NPV проекта. Напомню формулу этого показателя:

Если денежные потоки, приведенные к текущему периоду, больше инвестированных денег (NPV > 0), то проект выгодный. В противном случае – нет. Другими словами, нам потребуется сделать в Excel следующее:

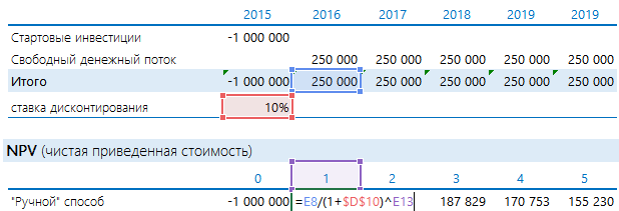
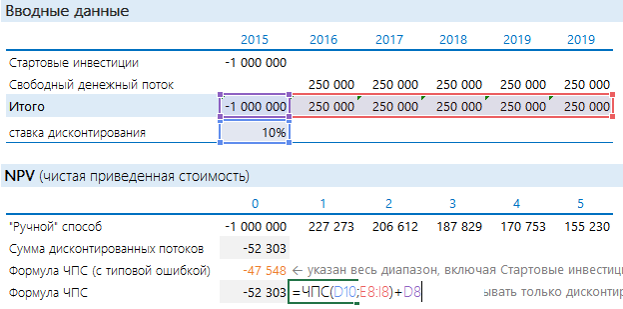
Добавить порядковые номера лет: 0 – стартовый год, к нему приводятся потоки. 1, 2, 3 и т.д. – это годы реализации проекта. В формуле на рисунке выполнены действия, которые прописаны выше после знака суммы (Σ): денежный поток за период делится на сумму 1 и ставки дисконтирования, возведенную в степень соответствующего года.

Рассчитанная строка представляет собой дисконтированный денежный поток. Чтобы получить значение NPV, достаточно найти общую сумму всей строки.

Получается «-52 303». Проект невыгоден.

Чтобы определить NPV, на самом деле необязательно готовить такую таблицу. Достаточно воспользоваться формулой Excel ЧПС. Синтаксис формулы такой (здесь и далее будет написано не как в справке Excel, а в переводе на понятный язык):

ЧПС(Ставка дисконтирования; Диапазон дисконтируемых значений)

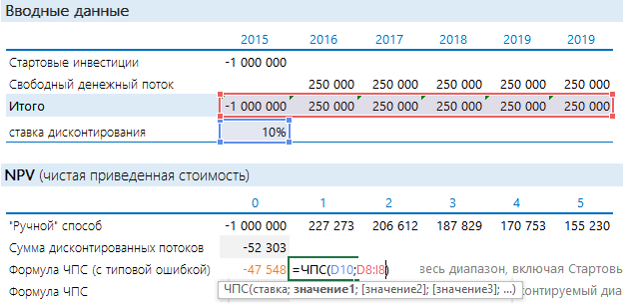
То есть достаточно указать ячейку с процентом и с денежными потоками. Но при использовании этой формулы с непривычки финансисты часто допускают ошибку:

Вообще-то дисконтированный поток и расчет по ЧПС должны совпадать. Почему же здесь разные значения? Дело в том, что ЧПС начинает дисконтировать с первого же значения. Т.е. она на самом деле ищет приведенную стоимость. А стартовые инвестиции нужно отнимать после. Правильная запись формулы в нашем случае будет иметь следующий вид:

Стартовые инвестиции «выведены» за пределы дисконтируемого диапазона и вычтены: т.к. стартовые инвестиции уже идут с минусом, то D8 нужно прибавлять. Теперь результаты одинаковые.

Оценка целесообразности проекта с помощью IRR

Как еще можно оценить проект? Можно посмотреть на него с точки зрения ставки дисконтирования. Задать вопрос: а какая должна быть ставка, чтобы NPV стала = 0? Вот этой ставкой как раз и является IRR. Если Ставка дисконтирования
Аннуитеты – любимая банковская цифра

Сначала поговорим о волнующем вопросе – как банки рассчитывают сумму равномерного платежа, как их проверить и как это понимать. Допустим, вы собираетесь взять кредит 1 000 000 руб. на 5 лет под 10% годовых. Платить будете раз в год равными платежами. Формулу из учебника по финансовому менеджменту здесь приводить не будем. Приведем формулу Excel:

ПЛТ(Ставка дисконтир; Количество периодов; Сумма кредита которую вы берете)

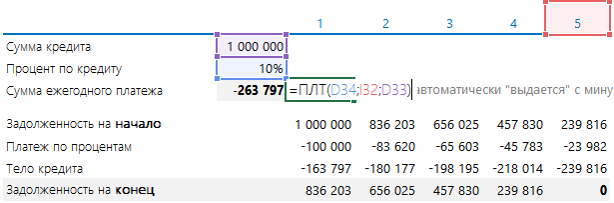
В формуле есть еще два необязательных пункта: сумма, которая должна остаться (по умолчанию ноль), и как высчитывать сумму – на начало месяца, и тогда ставят 1, или на конец – ставят ноль. В 90% случаев эти пункты не нужны, поэтому их можно не ставить вообще. Итого аннуитет определяется так:

Сумма ежегодного платежа получается сразу с минусом. Эту сумму нужно каждый год платить банку.

В ней содержатся две части: 1) платеж по кредиту, 2) тело кредита.

Ниже они показаны. Платеж по кредиту берется как 10% (процент по кредиту) от суммы задолженности на начало периода. Тело – как разность между ежегодным платежом и платежом по процентам (в Excel можно найти формулы, которые рассчитают вам и эти платежи). Задолженность на конец рассчитывается как разность между Задолженностью на начало и платежом по телу кредита.

Если платежи не ежегодные, а ежемесячные или ежеквартальные, то нужно ставку и период приводить к этим значениям. Так если бы у нас платеж был каждый месяц, формула выглядела бы так:

Мы бы годовую ставку разделили на 12 (привели к ежемесячному), и взяли не 5 периодов, а 5 • 12 = 60 месяцев. И получили ежемесячный платеж в 21 247 руб.

Нюансы и тонкости

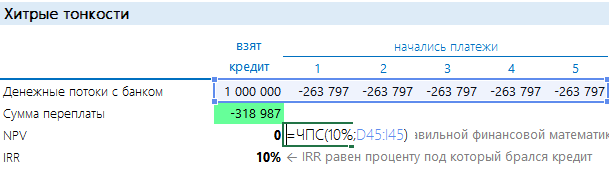
А теперь обсудим, как проверять банки на честность. Любой поток платежей по кредиту подразумевает под собой, что все выбытия денег приведены к поступлениям на ставку кредитования. Теперь по-русски: если мы построим денежный поток из полученного нами кредита и последующих наших аннуитетных платежей, то затем мы можем посчитать по ним NPV и IRR. NPV при этом должно принять нулевое значение, а IRR, что интереснее, — показать нам реальную процентную ставку.

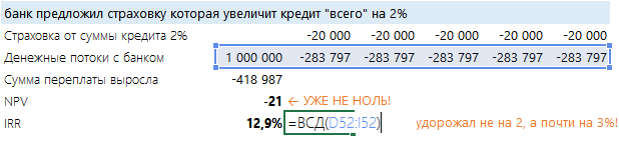
Когда кредит и платежи по нему рассчитаны правильно, то NPV, взятый по той же процентной ставке, равен нулю. А IRR показывает ставку. Когда банк делает предложение, от которого невозможно отказаться и которое увеличит кредитную ставку «всего» на несколько процентов – не верьте и пересчитывайте! Например, в нашем случае банк предложил страховку «всего» 2 % от суммы кредита в год. Думаете это прирост всего в 2%? Нет! Дело в том, что настоящий кредит в начале каждого года уменьшается:

В результате видно, что NPV не равен нулю. А реальный процент не 10, а 12,9%! Обратите внимание: здесь же выросла сумма переплаты. Если вас это смутит, вам могут предложить «еще более выгодные условия» — заплатить переплату сейчас, а остальное потом, меньшими платежами, или в нашем примере просто заплатить больше, а потом меньше. Сумма переплаты не изменится, а вот процент…

Что здесь сделано? Из каждого последующего платежа взята сумма 43 797 руб. и добавлена к первому же платежу (а бывает выкручивают сумму в момент выдачи кредита). Если для реального сектора финансовая математика «деньги вчера – деньги завтра» кажется несколько отдаленной от жизни, для банков это реальная прибыль. Поэтому всеми силами нагружают первый платеж. А вы с помощью простых формул сможете подготовить основу для дальнейших переговоров.

Да, не забудьте, если речь идет про ежемесячные платежи, умножать на 12.

Источник

Оценим инвестиционный проект

Задача по экономике:

Расчет NPV, PI, срока окупаемости простого, срока окупаемости дисконтированного, индекса рентабельности инвестиций, внутренней нормы доходности.

Дано: Инвестиции в бизнес составили 500 тыс. рублей.

Ожидаемые доходы (CFi) за 5 лет составят:

2014 год – 100 тыс. рублей. 2015 год – 150 тыс. рублей.

2016 год – 200 тыс. рублей. 2017 год – 250 тыс. рублей.

2018 год – 300 тыс. рублей.

Ставка дисконтирования 20%.

1. чистый дисконтированный доход (NPV) за 5 лет,

2. индекс прибыльности (PI) ,

3. сроки окупаемости простой и дисконтированный,

4. внутреннюю норму доходности (IRR).

Сначала рассчитаем чистые денежные потоки по формуле CFi/(1+r) t

Где CFi – денежные потоки по годам.

r – ставка дисконтирования.

t – номер года по счету.

Тогда в первый год чистый денежный поток будет равен CFi/(1+r) t = 100000 /(1+0,2) 1 =83333,33 рублей.

Во второй год чистый денежный поток будет равен CFi/(1+r) t = 150000 /(1+0,2) 2 = 104166,67 рублей.

В третий год чистый денежный поток будет равен CFi/(1+r) t = 200000 /(1+0,2) 3 = 115740,74 рублей.

В четвертый год чистый денежный поток будет равен CFi/(1+r) t = 250000 /(1+0,2) 4 = 120563,27 рублей.

В пятый год чистый денежный поток будет равен CFi/(1+r) t = 300000 /(1+0,2) 5 = 120563,27 рублей.

Где I – сумма инвестиций.

∑CF_i/(1+r) i – сумма чистых денежных потоков.

∑CF_i/(1+r) i =83333,33+104166,67+115740,74+120563,27+120563,27 =544367,28 рублей.

NPV=83333,33+104166,67+115740,74+120563,27+120563,27 – 500000 = 44367,28 рублей.

NPV= 44367,28 рублей.

NPV должен быть положительным, иначе инвестиции не оправдаются. В нашем случае NPV положителен.

Рассчитаем индекс рентабельности PI (profitability index).

Индекс рентабельности рассчитывается по формуле:

(чистые денежные потоки делим на размер инвестиций).

Тогда индекс рентабельности будет = 544367,28 / 500000=1,09.

Если индекс рентабельности инвестиций больше 1, то можно говорить о том, что проект эффективен.

Обобщим данные расчета NPV в таблице.

Рассчитаем срок окупаемости простой.

Инвестиции 500000 рублей.

В первый год доход 100000 рублей, т.е. инвестиции не окупятся.

Во второй год доход 150000 рублей, т.е. за два года доходы составили 250000 рублей, что меньше суммы инвестиций.

В третий год доход 200000 рублей, т.е. за три года доходы составили 250000+200000=450000 рублей, что меньше суммы инвестиций.

В четвертый год доход 250000 рублей, т.е. за четыре года доходы составили 450000+250000=700000 рублей, что больше суммы инвестиций.

Т.е. срок окупаемости простой будет 3 с чем-то года. Найдем точное значение по формуле.

Срок окупаемости простой =3+(остаток долга инвестору на конец третьего года) / денежный поток за четвертый год.

Срок окупаемости простой = 3+50000 /250000=3,2 года.

Рассчитаем срок окупаемости дисконтированный.

Инвестиции 500000 рублей.

В первый год чистый денежный поток 83333,33 рублей, т.е. инвестиции не окупятся.

Во второй год чистый денежный поток 104166,67 рублей, т.е. за два года дисконтированные доходы составили 83333,33+104166,67=187500 рублей, что меньше суммы инвестиций.

В третий год чистый денежный поток 115740,74 рублей, т.е. за три года дисконтированные доходы составили 187500+115740,74=303240,74 рублей, что меньше суммы инвестиций.

В четвертый год чистый денежный поток 120563,27 рублей, т.е. за четыре года дисконтированные доходы составили 303240,74+120563,27=423804,01 рублей, что меньше суммы инвестиций.

В пятый год чистый денежный поток 120563,27 рублей, т.е. за 5 лет дисконтированные доходы составили 303240,74+120563,27=544367,28 рублей, что больше суммы инвестиций.

Т.е. срок окупаемости дисконтированный будет больше 4, но меньше 5 лет. Найдем точное значение по формуле.

Срок окупаемости дисконтированный =4+(остаток долга инвестору на конец четвертого года) / чистый денежный поток за пятый год.

Срок окупаемости простой = 4+76195,99 / 120563,27 = 4 , 63 года.

Рассчитаем внутреннюю норму доходности.

Внутренняя норма доходности – это значение ставки дисконтирования, при которой NPV=0 .

Можно найти внутреннюю норму доходности методом подбора. В начале можно принять ставку дисконтирования, при которой NPV будет положительным, а затем ставку, при которой, NPV будет отрицательным, а затем найти усредненное значение, когда NPV будет равно 0.

Мы уже посчитали NPV для ставки дисконтирования, равной 20%. В этом случае NPV = 44367,28 рублей.

Теперь примем ставку дисконтирования равной 25% и рассчитаем NPV.

NPV= 100000/(1+0,25) 1 +150000/(1+0,25) 2 +200000/(1+0,25) 3 + 250000 / (1+0,25) 4 + 300000 / (1+0,25) 5 — 500000= -20896 рублей.

Итак, при ставке 20% NPV положителен, а при ставке 25% отрицателен. Значит внутренняя норма доходности IRR будет в пределах 20-25%.

Внутренняя норма доходности. Расчет

Найдем внутреннюю норму доходности IRR по формуле:

Данный пример предназначен для практических занятий. к.э.н., доцент Одинцова Е.В.

Источник

МСФО, Дипифр

Сравнение NPV и IRR. Модифицированная внутренняя норма доходности MIRR.

Два основных метода оценки инвестиционных проектов — это NPV и IRR (чистая приведенная стоимость и внутренняя норма доходности). Оба метода основаны на дисконтировании денежных потоков от проекта: NPV рассчитывает приведенную стоимость проекта при заданной ставке процента, IRR — дает представление о том, какая максимальная ставка кредита может быть принята для того, чтобы проект не был убыточным. Как пишут в учебниках финансового анализа, топ-менеджеры большинства компаний предпочитают оценивать потенциальные инвестиционные проекты в терминах % ставок доходности (т.е. IRR), а не в денежных суммах, приведенных к сегодняшнему моменту (т.е. NPV). И это вполне объяснимо.

Так можно ли говорить о преимуществах одного метода над другим, и какой метод лучше?

Почему IRR так любят менеджеры?

На самом деле, нет ничего удивительного в том, что внутренняя норма доходности (IRR) чаще используется на практике. Этому есть простое объяснение:

• использование IRR не подразумевает определение ставки дисконтирования, которая нужна чтобы рассчитать NPV проекта.
• удобно оперировать процентными ставками, а не какой-то абстрактной суммой денежных единиц (рублей), поскольку % внутренней нормы доходности можно легко сравнить со ставкой банковского кредита (хотя это и не совсем корректно)
• не правда ли: фраза «20% годовых» звучит гораздо более завлекательно, чем фраза «приведенная стоимость проекта равна 899 рублям».

Конечно же, первый пункт из этого списка самый важный. Потому что определение стоимости капитала для компании (так называемая WACC), которая используется при расчете NPV, само по себе является непростой задачей.

И да, высокое значение внутренней нормы доходности (например, 20%) производит сильное впечатление на слушателя и кажется заманчивым, однако все эти эпитеты из области эмоций. А инвестиции — это не та категория, которая может оцениваться на основе критериев «привлекательности».

В любом учебнике написано, что NPV метод предпочтительнее, так как он показывает величину добавочной стоимости, которую создает инвестиционный проект. IRR является относительным показателем, который показывает только при какой стоимости капитала мы получим нулевую добавочную стоимость. Может быть не стоит беспокоиться, и оба метода всегда дадут одинаковый ответ?

Когда методы NPV и IRR приведут к разным выводам?

Для независимых друг от друга проектов методы IRR и NPV всегда подскажут одно и то же решение: «принять» или «отклонить». Но мы живем в мире, где финансовые ресурсы (и не только они) ограничены. И всегда приходится выбирать между двумя взаимоисключающими проектами (построить дорогу в Якутии или отремонтировать мост в Волгограде). В этом случае нередки ситуации, когда метод IRR будет говорить нам, что стоит принять проект А, тогда как метод NPV будет «голосовать» за проект Б.

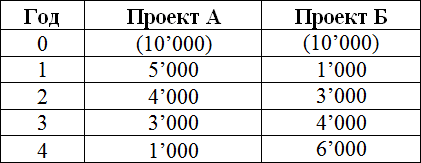
Возвращаясь к примерам из предыдущих статей про NPV и IRR, если проекты А и Б являются взаимоисключающими, то метод IRR всегда выберет проект А, так как 14,5%>11,8%. Но при ставке дисконтирования равной, например, 6% показатель NPV укажет на проект Б как на более предпочтительный:

• при стоимости капитала 10% NPV проекта А равно 788 денежных единиц, что больше, чем показатель NPV для проекта Б — 491 денежных единиц. Поэтому должен быть принят проект А!
• при стоимости капитала 6% NPV проекта А равно 1,588 денежных единиц, что меньше, чем показатель NPV для проекта Б — 1,724 денежных единиц. Поэтому должен быть принят проект Б!
• IRR не зависит от стоимости капитала, поэтому если использовать этот показатель, то всегда проект А будет выглядеть предпочтительнее

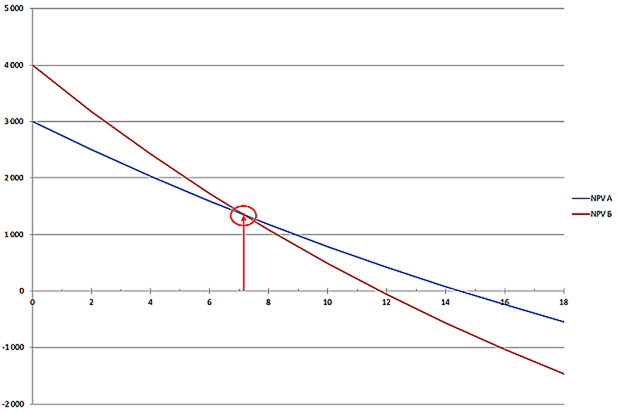
NPV и IRR будут рекомендовать разные проекты из двух возможных при стоимости капитала меньше, чем 7,2% (см. рис ниже).

Именно в этой точке (7,2%) графики зависимости NPV от ставки дисконтирования для проектов А и Б пересекаются между собой. Левее этой точки линия проекта Б ( красная ) выше, чем линия проекта А ( синяя ). Это значит, что при такой стоимости капитала (ниже 7,2%) проект Б сделает инвестора богаче, чем проект А.

О причинах такого положения дел я рассказывала в статье про расчет NPV инвестиционных проектов. Проект Б является долгосрочным, т.е. с течением времени денежные потоки от него увеличиваются. Проект А является краткосрочным с наибольшей отдачей в первые годы, а к концу проекта А поступления падают. Но чем дальше в будущее по времени от сегодняшнего момента, тем сильнее влияние ставки дисконтирования: через год увеличение ставки дисконтирования на 1% «съедает» 0,93% от денежного потока, а через 4 года рост ставки дисконтирование на 1% вызывает уменьшение денежного потока на 3,65%. Поэтому NPV долгосрочного проекта Б с ростом ставки дисконтирования падает быстрее, чем NPV проекта А, чьи денежные потоки максимальны в первые годы проекта. Это наглядно видно на рисунке: график проекта Б круче, чем график проекта А.

Получается, что методы NPV и IRR будут рекомендовать разные инвестиционные проекты, если есть разница по величине денежных потоков и по тому, как они распределены во времени: большие по величине в начале проекта или в конце. Это заложено в математику самого процесса дисконтирования.

Дело в том, что ставка дисконтирования работает в обе стороны времени — из будущего в настоящее (дисконтирование) и из настоящего в будущее (наращение). То есть если мы дисконтируем по 10% годовых, двигаясь из будущего к сегодняшнему дню, то мы можем и наращивать приведенные денежные потоки от сегодняшнего момента в будущее по этой же ставке. Внутренняя норма доходности, которую мы посчитаем методом IRR — это и ставка дисконтирования, и ставка инвестирования.

Так вот — когда мы рассчитываем IRR, мы предполагаем, что все денежные потоки инвестируются по этой ставке (как описано в примере про банковский депозит, его IRR равна ставке по депозиту).

Когда мы рассчитываем NPV, мы предполагаем, что денежные потоки дисконтируются и инвестируются по стоимости капитала компании. И это является более правильным с экономической точки зрения. Если мы получим IRR, равную 20%, это не означает, что мы можем найти банк или проект, который принесет нам ровно такую ставку доходности.

Все взаимоисключающие инвестиционные проекты с различающимися по времени денежными поступлениями правильнее сравнивать с помощью показателя NPV, который покажет вам прирост вашего богатства в абсолютной величине, а не потенциальную внутреннюю доходность, которую вы никогда, возможно, и не получите. Метод IRR для таких проектов может привести к неверному выбору, как в нашем примере при ставке 6%.

Еще достоинствах и недостатках метода IRR

Преимуществом показателя IRR является возможность оценить «запас прочности» проекта (safety margin) перед возможным увеличением процентных ставок. Например, в России кредитные ресурсы одномоментно стали дороже на несколько процентов, когда в ночь на 16 декабря 2014 года Центробанк РФ резко повысил ставку рефинансирования до 17%. Если бы мы приняли проект А, IRR которого равна 14,5%, то в этом случае он за одну ночь стал бы нерентабельным. А если бы мы нашли проект с внутренней нормой доходности равной 20%, то даже такое резкое увеличение процентных ставок не сделало бы наш проект убыточным.

К недостаткам метода внутренней нормы доходности относится тот факт, что для нестандартных проектов могут быть получены несколько величин IRR. Стандартный проект — это когда есть один отрицательный денежный поток в самом начале (первоначальная инвестиция) и несколько положительных денежных потоков в будущем. Если положительные и отрицательные денежные потоки будут чередоваться, то математически мы получим столько IRR, сколько раз денежные потоки от проекта поменяют знак.

Например, для проекта с такими потоками: (10,000), 5 000, (2 000), 4000, 5 000 будет получено два показателя IRR.

MIRR модифицированная внутренняя норма доходности — что это?

Анализ инвестиционных проектов на основе метода внутренней ставки доходности (IRR) предполагает, что все денежные потоки проекта могут быть инвестированы по этой ставке, что нереально. Этот недостаток метода IRR устраняется при использовании так называемой модифицированной внутренней нормы доходности или сокращенно MIRR (Modified Internal Rate of Return).

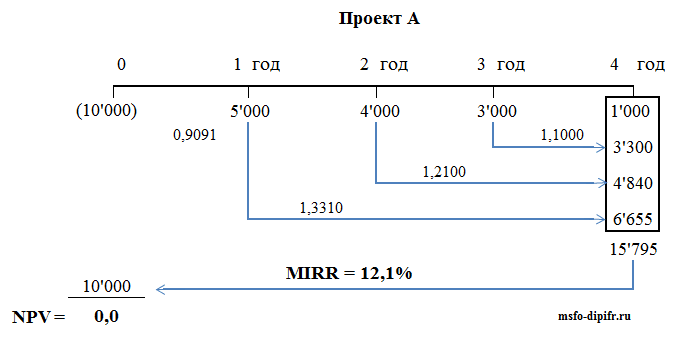
Суть расчета MIRR проста: все положительные денежные потоки от проекта наращиваются по % ставке, равной стоимости капитала компании (WACC), а затем находится ставка, дисконтируя по которой мы получим сумму нашей инвестиции. Возьмем для примера проект А, тот же самый, который использовался для расчета NPV и IRR ранее. Чтобы разобраться, как сделать расчет модифицированной внутренней нормы доходности, посмотрите на рисунок ниже:

Разберем всё по порядку.

Действие первое: все потоки от проекта инвестируются (наращиваются) по ставке 10% (мы помним, что это стоимость капитала для нашей компании).

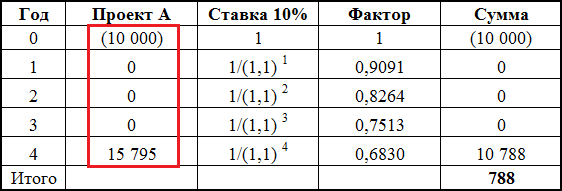
Последний денежный поток не наращивается, это будет датой окончания нашего инвестиционного проекта. Итого получилось в четвертый год суммарный денежный поток должен быть равен 15,795.

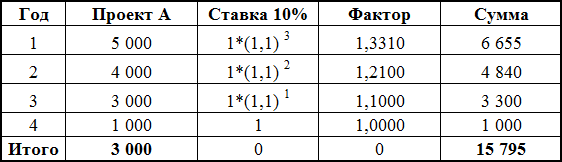
После этого денежные потоки от проекта будут такими (в красной рамке):

В этой таблице рассчитан NPV проекта после «модифицирования» его денежных потоков. Как видно из таблицы, ничего не поменялось: NPV проекта А как и раньше равно 788 денежным единицам.

То есть у нас получилось, что вместо ежегодных денежных притоков остался только один положительный денежный поток в конце 4-го года и первоначальная инвестиция в сумме 10,000. Единственный денежный приток является эквивалентом четырех ежегодных положительных денежных потоков, что подтверждается неизменностью величины NPV.

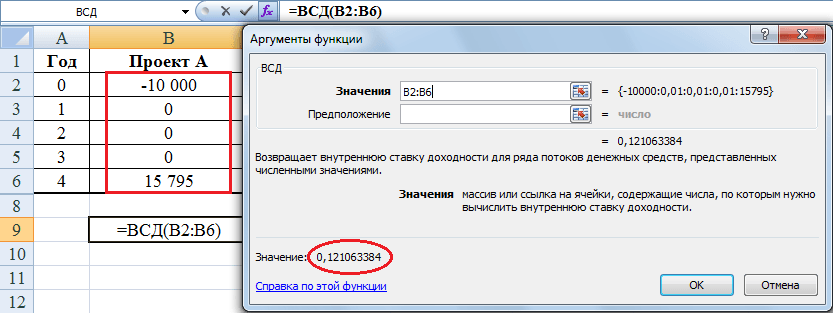
Действие второе: теперь надо вычислить внутреннюю норму доходности для этих двух денежных потоков, которые эквивалентны первоначальному проекту А. Для этого лучше всего воспользоваться функцией ВСД в программе Excel (об этом подробно рассказано тут):

IRR в данном случае получилось равной 12,1%, а не 14,5% как IRR для первоначального проекта А. Эта величина 12,1% и является модифицированной внутренней нормой доходности.

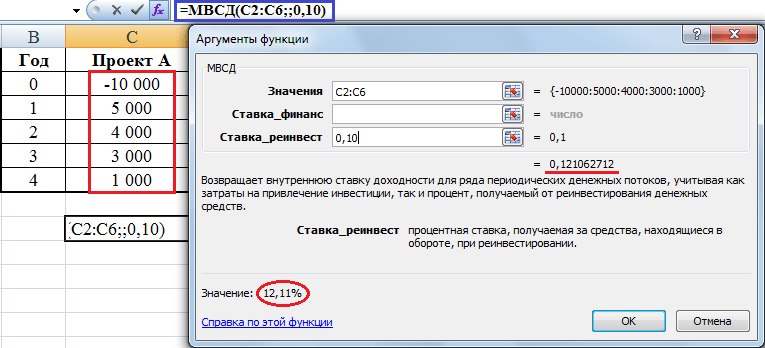
В программе Excel можно рассчитать показатель MIRR напрямую. В закладке Формулы—>Финансовые есть формула МВСД, которая и отвечает за расчет модифицированной нормы доходности. В ячейку «значение» нужно ввести ссылку на ячейки с денежными потоками, в ячейку «ставка_реинвест» — значение стоимости капитала, в нашем случае 10%.

Как видно из рисунка, функция МВСД дает то же самое значение показателя MIRR, которое было получено ранее расчетом из двух действий, а именно 12,1%.

Теперь можно посмотреть, как изменится решение о выборе из двух инвестиционных проектов А и Б.

Как видно из таблицы, при стоимости капитала (ставке дисконтирования и инвестирования) 10% оба метода «выбирают» проект А, при стоимости капитала 6% — оба метода также «голосуют» за один и тот же проект — проект Б (выделено синим). Сравните эту таблицу с предыдущей, где при тех же % ставках сведены вместе показатели NPV и IRR (ссылка на эту таблицу).

Таким образом, метод модифицированной внутренней нормы доходности снимает конфликт между NPV и IRR при выборе между двумя взаимоисключающими проектами, поскольку уравнивает ставку реинвестирования денежных потоков. Однако, MIRR отменяет одно из преимуществ метода IRR — придется рассчитывать ставку дисконтирования равную стоимости капитала компании, что всегда вызывает затруднения.

Возможность принятия противоположных решения также сохраняется. Если два проекта имеют одинаковый масштаб и продолжительность, то да, методы NPV и MIRR всегда будут выбирать один и тот же проект из двух взаимоисключающих проектов. То же самое справедливо и в отношении проектов одинакового размера, но разной продолжительности. В этом случае надо рассчитывать эти показатели на основе самого длительного проекта, просто добавив нулевые денежные потоки к более короткому проекту. Однако, если взаимоисключающие проекты различаются по масштабу (величине денежных потоков), то конфликт между двумя методами все еще возможен. Поэтому применение метода NPV все-таки является предпочтительнее, чем расчет IRR или MIRR (обычной или модифицированной внутренней нормы доходности).

«Сделай шаг, и дорога появится сама собой». Стив Джобс

Если вы раздумываете над тем, надо ли что-то сделать или следует получше подготовиться — не тратьте всю жизнь на сомнения. Можно бесконечно анализировать информацию, просчитывать варианты, оценивать риски и строить графики зависимости результата от самых разных показателей. Но всё дело в том, что точно предсказать будущее не может никто.

Вы можете всё время откладывать начало проекта в ожидании лучших условий — более низких ставок по кредиту, роста экономики, укрепления курса национальной валюты. Однако, не надейтесь, что дождетесь идеальных условий для старта, они никогда не наступят. Потому что когда исчезает одно препятствие, вместо него всегда появляется другое. Идеальный день для начала любого проекта — это сегодня.

«Теоретики беспокоятся о том, чтобы принять хорошее решение. В бизнесе мы так же беспокоимся о том, чтобы сделать решения хорошими».

Нужно принимать решение, опираясь на ту информацию, которая имеется в наличии сегодня. По дороге к мечте всё равно придётся вносить коррективы, чтобы добиться результата. Самый лучший прогноз всегда оказывается неверным. Потому что невозможно предсказать последствия как ваших действий, так и изменения окружающей обстановки с течением времени. Это можно сделать только в единственном случае — если вы ничего не делаете.

В мире бизнеса имеет значение результат, а не бизнес-планы. Впрочем, это относится к любым сторонам нашей жизни. Никого не интересуют мечты, важно, сумели ли вы до них дотянуться.

«Каждый раз нужно прыгать со скалы и отращивать крылья по пути вниз». Рэй Брэдбери

Лучше и не скажешь.

Другие статьи из рубрики «Финансы»:

Источник