Как рассчитать среднюю доходность классов активов

Как рассчитать среднюю доходность классов активов

Как не ошибиться, рассчитывая среднюю доходность инвестиций, что такое «подножка волатильности», и почему умелая диверсификация не только обеспечивает стабильность инвестиционного портфеля, но и улучшает доходность.

Все инвесторы сталкиваются с необходимостью расчета средней доходности своего портфеля. Это нужно для того чтобы прогнозировать его будущую стоимость. Без такого прогноза невозможно, например, решить, на какую сумму следует пополнять инвестиционный портфель, чтобы достичь поставленных целей к сроку.

Часто инвесторы ошибаются в расчетах, потому что используют неправильную формулу. Использовать ошибочную оценку в планировании будущих действий опасно. Ценой просчета может стать качество жизни в старости или образование ребенка.

Как правильно оценить среднюю доходность

Среднюю доходность портфеля в заданном периоде нужно считать не как среднюю арифметическую, а как среднюю геометрическую. Разберемся на простом примере.

Допустим инвестор вкладывает деньги в российские акции через фонд А и российские облиции через фонд Б в пропорциях 60 на 40. Ниже в таблице приведены данные по ежегодной динамике стоимости акций, облигаций и совокупного портфеля.

Таблица №1. Доходности фондов А, Б и портфеля 60/40 за 4 года (в руб).

Инструмент	2016	2017	2018	2019
Фонд А	28,67%	-2,22%	16,74%	37,44%
Фонд Б	15,24%	14,83%	2,7%	15,34%
Портфель 60/40	23,30%	4,60%	11,12%	28,60%

Акции, облигации и портфель за все время принесли 101,86%, 56,74% и 83,81%. На первый взгляд получается 20,16%, 12% и 16,9% в среднем за год. На самом же деле эти цифры завышены. Как так вышло? Дело в том, что арифметическая средняя (сумма доходностей, поделенная на количество периодов) не походит для расчета инвестиционных результатов, так как доходность, полученная в очередном периоде, относится к стоимости портфеля в предыдущем периоде, и включает доходность на доходность прошлого периода, а не только на сумму инвестиций. Например, если портфель упал на 5% за период с уровня 10000, а затем поднялся на 5%, он не вернется к 10000, а будет стоить 9975 руб. В этом примере разница небольшая, но чем больше рыночная нестабильность, то тем больше будет расхождение. — это прекрасно видно на примере фонда А, который является более волатильным, чем фонд Б.

Для того, чтобы правильно учесть волатильность доходностей и их влияние на результат используют среднюю геометрическую или, как еще её называют, аннуализированную доходность (Compound Average Growth Rate). Она рассчитывается как корень степени n из произведения доходностей за n периодов. Например, ∜(1,232 * 1,046 * 1,1112 * 1,286) даст среднюю доходность портфеля в 16,5% в год (а не 16,7%, как средняя арифметическая). Как и средняя арифметическая, средняя геометрическая не всегда соответствует показателю в каждый конкретный год, но при этом в конце периода она трансформирует первоначально инвестированную сумму в точный итоговый результат инвестирования. Как следствие, именно этот показатель, а не среднюю арифметическую доходность стоит использовать для долгосрочного инвестиционного планирования. Сравнение динамики средней арифметической и реальной доходностей представлены в таблице №2 и на графике №1.

График №1. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Таблица №2. Динамика средней арифметической и реальной стоимости портфеля (в руб).

Источник: Bloomberg, расчеты FinEx

Что такое подножка волатильности?

Разницу между средней арифметической и средней геометрической доходностью в академических кругах называют «volatility drag» или «подножка волатильности». Почему же речь идет о «подножке»? Потому что с точки зрения математики, чем более волатилен ряд доходностей, тем сильнее геометрическая доходность будет отставать от арифметической.

Volatility Drag = средняя арифметическая доходность — средняя геометрическая доходность

Несмотря на свою простоту, это формула позволяет сделать ряд интересных выводов — например, относительно опасности популярных у многих инвесторов инвестиций с использованием заемных средств («финансового рычага»). Когда инвестор рискует не только собственными средствами, но и занимает дополнительные деньги у своего брокера для того, чтобы увеличить размер своего портфеля, он увеличивает и его волатильность.

Например, использование рычага 2 (на каждый вложенный собственный рубль инвестиций инвестор получает в кредит еще один рубль и инвестирует его в рынок) обеспечивает удвоение арифметической доходности (без учета расходов в связи с использованием рычага). Но в случае падения, удваиваются и потери. В результате из-за бремени волатильности средняя геометрическая доходность меняется медленнее.

Как диверсификация отражается на волатильности портфеля?

Диверсификация портфеля сокращает volatility drag и поэтому положительно сказывается на доходности портфеля. Рассмотрим простой пример: инвестор может инвестировать в акции компании А или в акции компании А и Б. Волатильность акций компании А 26%, Б – 11%, их годовые доходности и результаты инвестирования для первого и второго случая представлены в таблице ниже. Как видно из таблицы, из-за большей волатильности первого инструмента, даже большие номинальные доходности несут в итоге результат хуже, чем в случае с инвестированием в разные инструменты даже пусть с меньшей общей доходностью. Это происходит как раз из-за того, что волатильность съедает большую доходность. Во втором случае портфель падает меньше чем при инвестировании исключительно в акции А, и даже небольшая доходность дает лучший итоговый результат в 6,7% за 10 лет.

График №2. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Источник: Bloomberg, расчеты FinEx

Таблица №3. Динамика портфеля только из акций компании А и портфеля из акций компаний А и Б в пропорции 50/50 (в руб).

Источник

Правильный расчет среднегодовой доходности в инвестициях

Любой инвестор рано или поздно должен подвести итоги и рассчитать доходность инвестиций. Так как цифры вроде 125% за 5 лет мало информативны, то доходность принято приводить доходность к годовым значениям. Такую доходность называют среднегодовой доходностью. В случае с 125% за 5 лет среднегодовая доходность равна 17,6%. 125% принято назвать накопленной доходностью.

Как рассчитать среднегодовую доходность

Если период инвестиций измеряется в годах, то формула среднегодовой доходности выглядит следующим образом:

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в годах)

Эта формула предполагает капитализацию процентов. Её нельзя применять, например, в тех случаях, когда дивиденды выводились из инвестиций (не реинвестировались).

В случае произвольного промежутка инвестиций среднегодовая доходность считается по аналогии.

R – накопленная доходность
r – среднегодовая доходность
T– срок инвестиций (в месяцах)

Здесь период инвестиций измеряется в месяцах. Если необходимо рассчитать с точностью до дней, то 12 надо заменить на 365.

Пример вычисления:

Инвестор получил доходность 12% за 16 месяцев. Чему равна его годовая доходность?

Основные ошибки при вычислениях

Чаще всего начинающие инвесторы допускают ошибку, считая следующим образом (пример с доходностью 125% за 5 лет):

Или в примере с 12% за 16 месяцев:

Такой вариант расчетов в инвестициях использовать нельзя, так как при этом не учитывается капитализация процентов.

Источник

Риск и доходность финансовых активов в России

Автор: Алексей Мартынов · Опубликовано 30.06.2016 · Обновлено 09.07.2016

Одной из важнейших характеристик класса активов являются его риск и доходность. В статье Asset Allocation про Риск и доходность я подробно описывал риск и доходность зарубежных классов активов. В этой статье я проанализирую российские активы: акции, облигации, золото и валюту. Какую долгосрочную доходность они приносили и какова степень их риска.

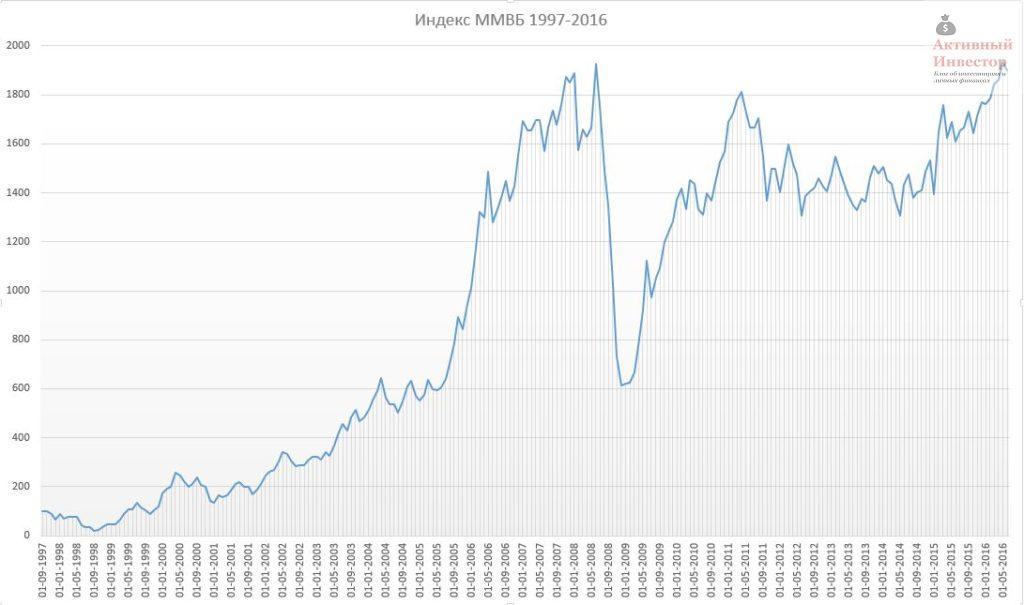
Акции. Индекс ММВБ.

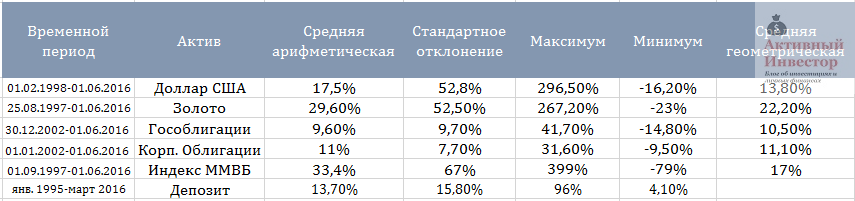
Индекс ММВБ начал отсчет 1 сентября 1997 года со 100 пунктов. С тех пор прошло почти 19 лет и 1 июня 2016 года значение индекса составило 1899 пункта, то есть он вырос почти в 19 раз. Перед тем, как оценить риск и доходность российского индекса, нужно провести небольшой ликбез, потому что доходность можно считать по разному.

Средняя арифметическая доходность — это когда рассчитывается среднее арифметическое значение множества доходностей за один и тот же период. Например, у нас есть доходность за каждый год за три года: +10%, +15%, -11%. Среднее арифметическое будет (10+15-11)/3=4,66%. Это показывает, какую в среднем можно было получить доходность за один год.

Средняя геометрическая доходность (CAGR) — это когда берется конечное и начальное значение индекса и рассчитывается, на сколько процентов он рос в среднем за год. Например, индекс вырос со 100 до 350 пунктов за 3 года. Геометрическая доходность будет равна частному 350/100, возведенному в степень 1/3, минус 1: ((350/100)ˆ1/3)-1 = 0,518 или 51,8%. Эта доходность в отличие от предыдущей учитывает сложный процент и показывает средний ежегодный рост за взятый промежуток времени. Если взять предыдущий пример, то геометрическая доходность рассчитывается так: ((1,1*1,15*0,89)ˆ1/3)-1 = 4%.

В качестве меры риска используется стандартное отклонение. Стандартное отклонение показывает в какой степени множество значений доходности отклоняется от среднего арифметического. Например, если СА 20%, а СО 40%, это означает, что в 70% случаев доходность лежит в диапазоне от -20% до +60%.

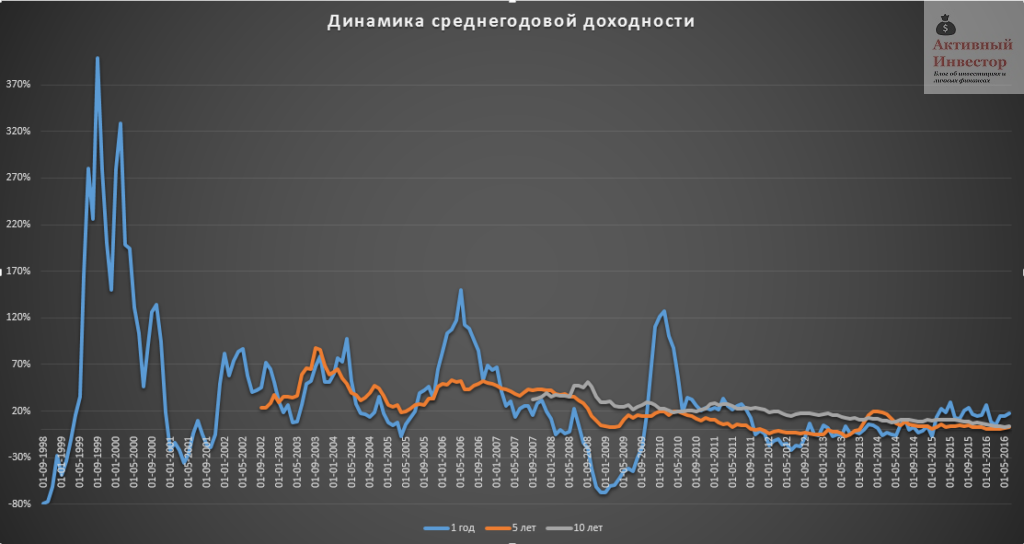
Теперь, когда мы разобрались в расчетах и отличиях, можно перейти к конкретным цифрам. с 1997 по 2016 год средняя арифметическая доходность индекса ММВБ за год составила 33,4%, стандартное отклонение 67%. Максимальное значение 399%, самое сильное падение -79%. Среднее геометрическое 17%, то есть в среднем индекс рос на 17% в год.

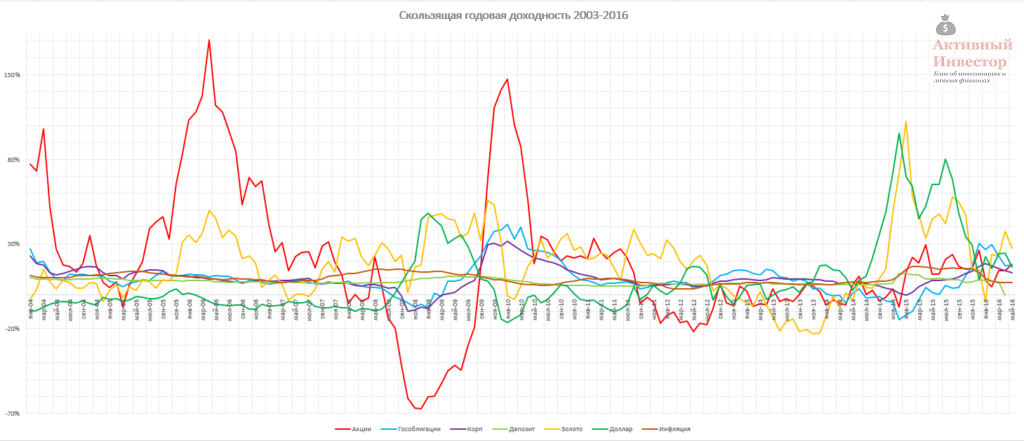
Для расчета я брал скользящую годовую доходность, например январь 2015-январь 2016, февраль 2015-февраль 2016 и так далее. Такая методика охватывает гораздо большее количество годовых периодов и позволяет более точно проанализировать риск и доходность инструмента в отличие от обычной методики, когда берется только доходность за календарный год, то есть от января к январю.

Однако, 1 год инвестирования — это очень маленький срок для акций. Далее я покажу, как меняется риск и доходность при инвестировании на более длительные сроки: 3 года, 5 лет, 8 лет и 10 лет. На графике ниже показана максимальная и минимальная среднегодовая доходность за выбранный период и среднее арифметическое этих доходностей. Можно заметить, что с увеличением срока инвестирование разброс доходностей сужается и стремится к среднему. Например, за 5 лет максимальная доходность составила 57% годовых, а минимальная -7%. При этом среднее арифметическое значение всех периодов лежит около 20%. Исключением является только срок инвестирования в 1 год, что говорит об очень высокой волатильности акций на таком коротком сроке.

На следующем графике можно визуально оценить динамику скользящей доходности. Годовая линия сильно колеблется, то сильно вырастая вверх, то сильно падая вниз. Основные колебания пришлись на кризисы — 1998 и 2008 год. Пятилетняя линия выглядит гораздо более сглаженной и плавной, а десятилетняя еще в большей степени. В последние периоды годовая доходность стремится к нулю, так как фактически с 2008 года индекс находится в боковике и только-только достиг прежних уровней спустя 9 лет.

Какие выводы можно сделать из этих цифр и графиков? Во-первых, чем больше срок инвестирования в акции, тем меньше стандартное отклонение и больше предсказуемость доходности. Во-вторых, с увеличением срока инвестирования уменьшается величина убытка и вероятность его получить. На сроке 10 лет не было ни одного убыточного периода. В-третьих, несмотря на большой потенциал доходности, на длительном сроке акции могут принести низкую доходность. Например, за те же 10 лет в худшем варианте можно было получить всего лишь 3% в среднем в год (без учета дивидендов).

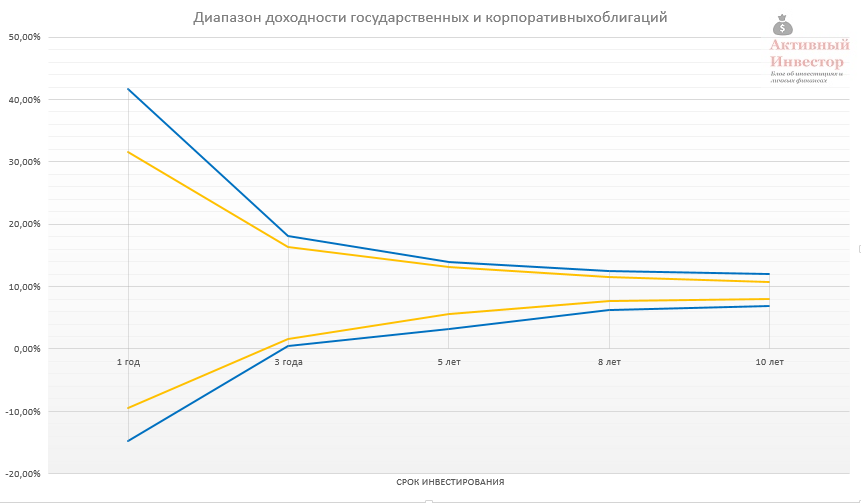
Российские облигации

Российские облигации можно поделить на несколько подклассов: государственные, муниципальные и корпоративные. Я рассмотрю только государственные и корпоративные. Государственные облигации (ОФЗ) выпускаются Министерством Российской Федерации и для отражения их динамики существует индекс московской биржи RGBI TR — это индекс полной (совокупной) доходности. Отсчет данного индекса начинается с 30 декабря 2002 года.

В качестве бенчмарка корпоративных облигаций я буду использовать индекс IFX Cbonds — это тоже индекс полной доходности, который начал свой отсчет на год раньше — 1 января 2002 года. Московская биржа так же ведет индекс корпоративных ценных бумаг MICEXBITR, но его динамика на мой взгляд почему-то аномальна, поэтому его я использовать не буду.

Средняя годовая арифметическая доходность ОФЗ составила 9,6%, стандартное отклонение 9,7%, средняя геометрическая 10,5%. За год максимум можно было получить 41,7%, в худшем случае падение составило -14,8%.

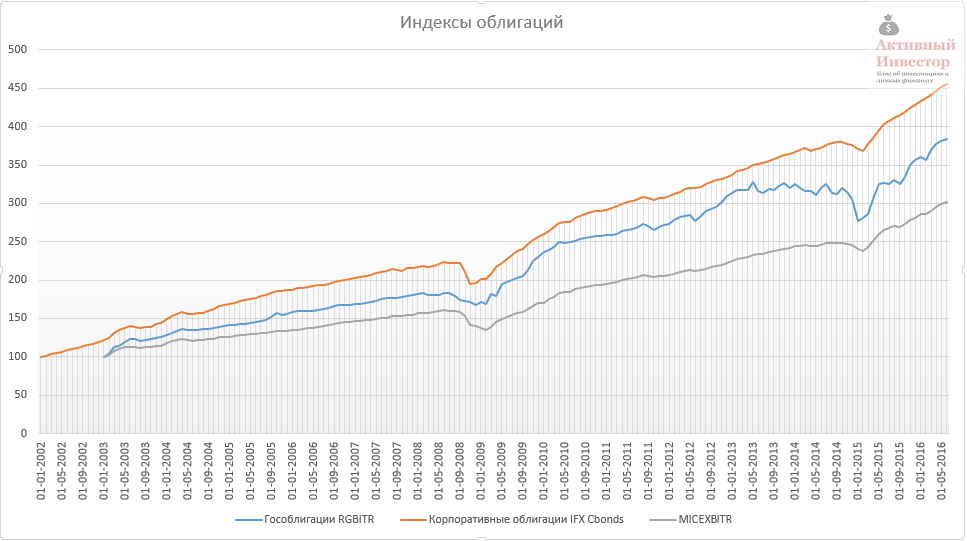
Корпоративные облигации приносили в среднем 11% в год, при риске 7,7%. Среднегодовой рост 11,1%.

C увеличением срока инвестирования диапазон доходности так же как и у акций снижается и стремится к средней. Однако даже по облигациям на сроке 3 года результат мог оказаться нулевым.

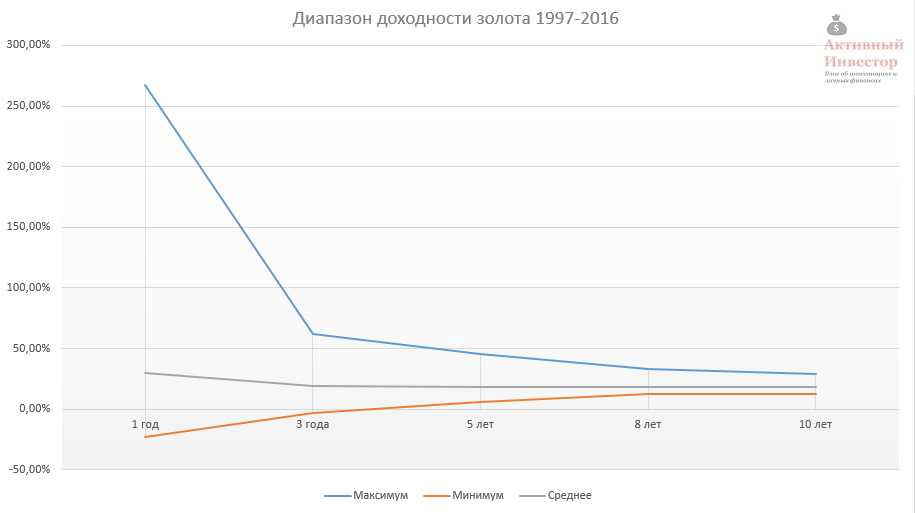
Золото

Цены на золото устанавливаются Центральным Банком РФ. На сайте ЦБ присутствуют данные, начиная с августа 1997 года.

Средняя арифметическая годовая доходность золота составила 29,6% при стандартном отклонении 52,5%. В лучшем случае за год можно было заработать 267,2%, в худшем получить убыток -23%. За почти 20 лет золото приносило 22,2% годовых.

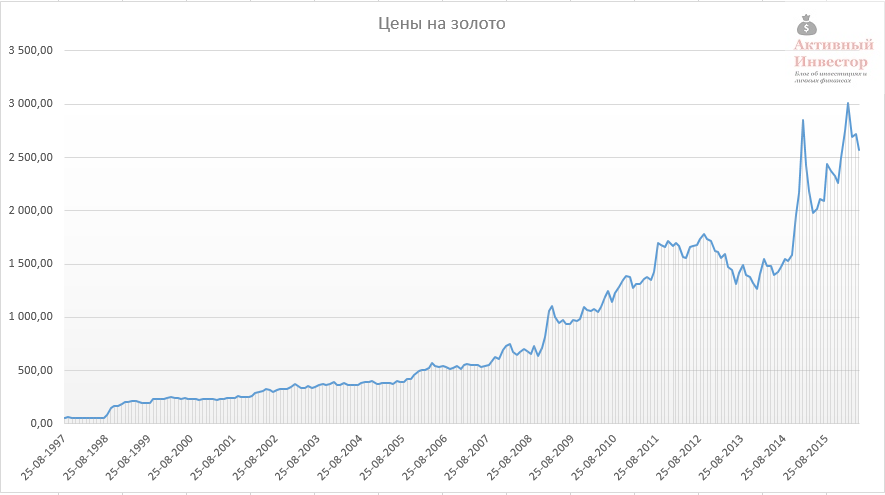
Максимум, который можно было бы получить за 3 года, составил 62% годовых, минимум -3%. За 10 лет максимум 29,4%, минимум 12,4%. Среднее значение доходности 18,6%.

Доллар США

Курс доллара США так же как и золото, рассчитывается Центробанком. На сайте присутствуют данные с февраля 1998 года.

На сроке 1 год средняя арифметическая доходность вложений в доллар США составила 17,5%, стандартное отклонение 52,8%. За год максимум можно было заработать 296,5%, в худшем случае -16,2%. Среднегодовой рост за 18 лет 13,8%.

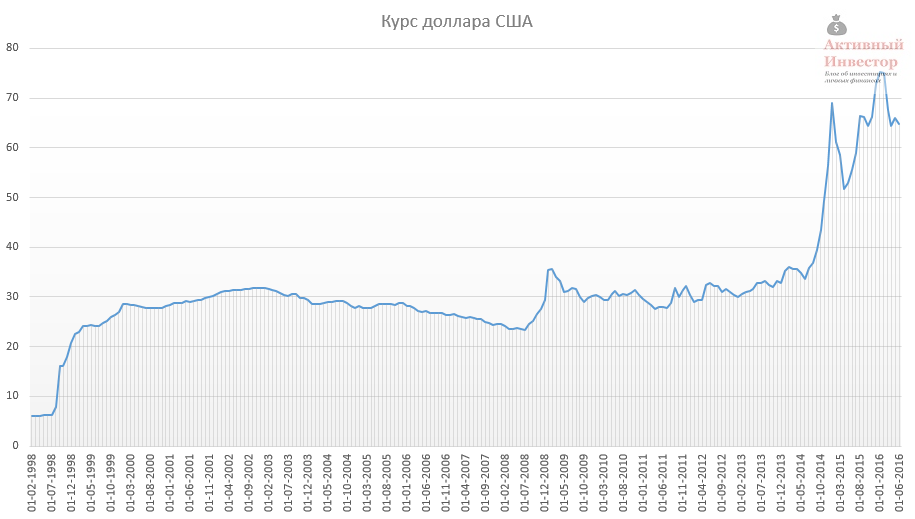
C увеличением срока инвестирования средняя падает до уровня 3-4% годовых.

Если объединить все классы активов в единую таблицу, то получится следующее:

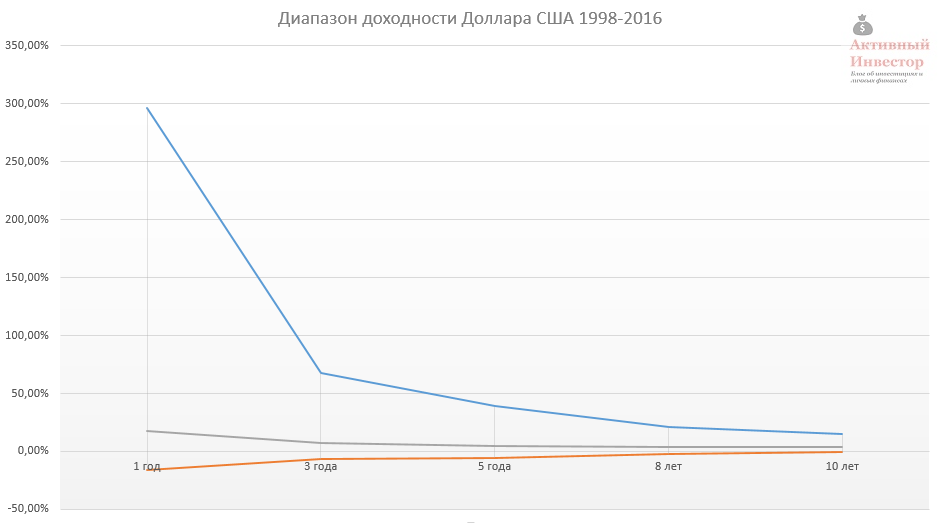
Доходность активов за 1 год инвестирования

Здесь я еще добавил доходность банковских депозитов начиная с 1995 года. В среднем депозиты со сроком на 1 год приносили 13,7% при стандартном отклонении 15,8%. Высокая средняя объясняется крайне высокими процентными ставками в 90-х годах. Например, в 95-м году можно было открыть вклад с космической по сегодняшним меркам доходностью 96%.

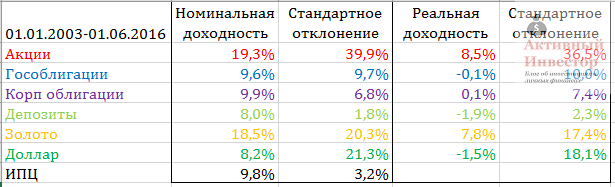
Однако такое сравнение инструментов не совсем корректное, так как неверно сравнивать доходность на различных временных интервалах. Разные экономические циклы и кризисы могут сильно влиять на значения риска и доходности. Поэтому ниже таблица, где сравниваются инструменты за один и тот же промежуток времени — с января 2003 года, который обусловлен началом отсчета индекса государственных облигаций. Этот отрезок времени уже не захватывает кризис 98 года, поэтому цифры доходности более умеренные.

Если брать среднегодовую доходность (CAGR), то на данном сроке лучше всего показало себя золото, на втором месте акции, в роли аутсайдера — доллар, несмотря на сильную девальвацию национальной валюты.

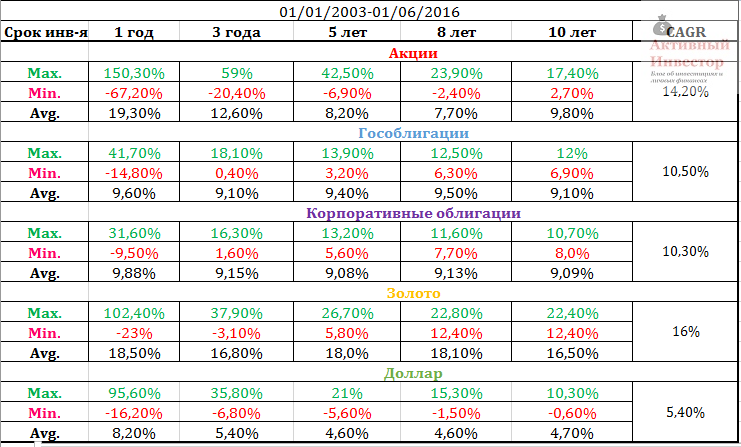
Чтобы нагляднее оценить волатильность доходности на сроке инвестирования 1 год можно взглянуть на этот график. На нем изображены годовые доходности каждого актива. Годовая доходность акций самая непостоянная и подвержена сильным колебаниям. Золото и доллар чуть более стабильны, но тоже могут сильно расти и падать.

Реальная доходность активов

Все вышеприведенные цифры — это номинальная доходность. Но номинальная доходность ничего не говорит о реальном увеличении вложений. Те же банковские депозиты с доходностью 96% в 1995-м году — это на первый взгляд очень много. Но при инфляции 131%, которая была в то время, это совсем мало. Поэтому нужно смотреть не номинальную, а реальную доходность, чтобы понять приносит актив реальную прибыль или нет. Прошу обратить внимание, что для расчета реальной доходности используется эта формула.

В таблице ниже показаны средние значения годовой доходности активов и инфляции. Среднее значение годовой инфляции с 2003 года составило 9,8%. В правой части таблицы посчитана реальная доходность активов. Для ее расчета из номинальной годовой доходности вычиталась инфляция за аналогичный период, после чего рассчитывалось среднее арифметическое множества результатов за весь период. Как видно, реальную доходность за указанный срок смогли принести только два актива — золото и акции. Все остальные показали результат либо на уровне либо хуже инфляции. В аутсайдерах доллар и депозиты.

Средняя доходность активов на сроке 1 год

Графически эту таблицу можно представить на диаграмме риск — доходность.

Если посчитать среднегодовые реальные темпы роста за этот же срок, то получатся следующие цифры. Инфляция за 13,5 лет составила 9,8%. Реальная доходность индекса ММВБ 4%, золота 5,6%. Результат облигаций на уровне инфляции, а доходность доллара отрицательная.

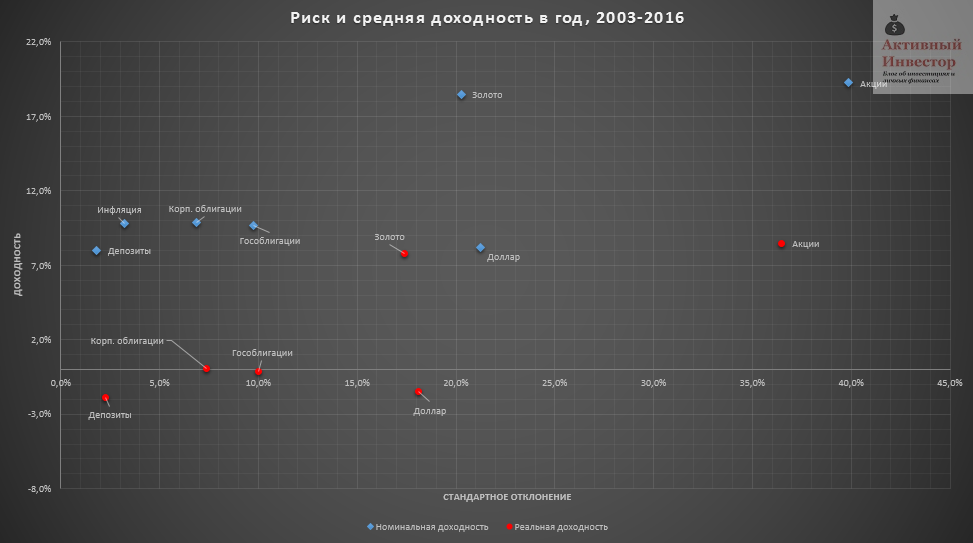
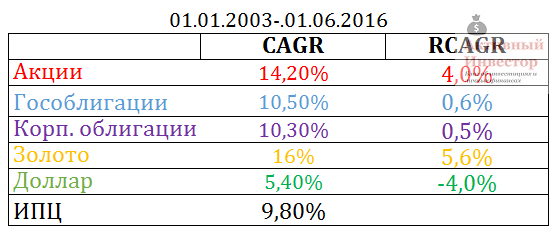
Среднегодовые темпы роста, реальные и номинальные

Напоследок замечу, что доходность индекса ММВБ не учитывает получение и реинвестирование дивидендов. С их учетом реальный рост индекса был бы на 2-3% больше. А доходность корпоративных облигаций не учитывает, что с купонного дохода платится налог.

Эти цифры можно сравнить с реальной долгосрочной доходностью зарубежных активов. Например, реальная доходность акций США почти равна реальной доходности индекса ММВБ с учетом дивидендов. А доходность зарубежных облигаций заметно больше реальной доходности российских. Золото на заданном отрезке времени в России было более выгодно, чем его долгосрочный результат зарубежом.

Следует еще отметить, что выбранный промежуток 2003-2016 по меркам долгосрочных инвестиций не такой уж и большой, и в будущем цифры могут поменяться. Но даже имеющиеся результаты можно использовать в своих прогнозах, а чем я расскажу в следующей статье.

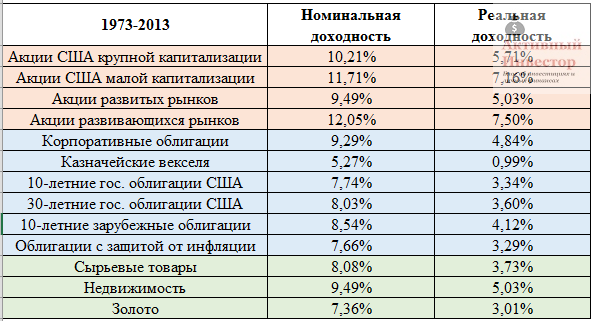
Источник