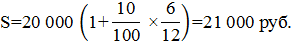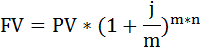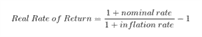Как рассчитать доходность вклада при инфляции

Типовая задача № 3. Депозитные операции с учетом инфляции

Вклад в сумме 20 000 руб. положен в банк на шесть месяцев. Ставка по вкладу 10% годовых. Уровень инфляции 5% в месяц. Определить сумму вклада с процентами, сумму вклада с процентами с точки зрения покупательной способности, реальный доход вкладчика, если:

1) Начисление производилось по схеме простых процентов;

2) Начисление производилось по схеме сложных процентов (ежемесячно).

Решение.1) По формуле (15) рассчитаем сумму вклада с процентами:

Для того, чтобы определить сумму вклада с точки зрения покупательной способности, т.е. с учетом инфляции за период депозита, необходимо рассчитать индекс инфляции по формуле (9):

Расчет суммы вклада с учетом инфляции выглядит следующим образом:

S_i = 21 000 / 1,3 = 16 153,8 руб.

Реальный (т.е. с учетом инфляции) доход вкладчика равен:

Д_р = S_i — 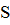= 16 153,8 – 20 000 = — 3846,2 руб. (реальный убыток).

2) По формуле (16) рассчитаем сумму вклада с процентами:

S = 20 000 (1 + 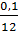) 6 = 22 000 руб.

Для того чтобы определить сумму вклада с точки зрения покупательной способности, т.е. с учетом инфляции за период депозита, необходимо рассчитать индекс инфляции по формуле (9):

С учетом инфляции сумма вклада будет равна:

S_i = 22 000 / 1,3 = 16 923,1 руб.

Реальный (т.е. с учетом инфляции) доход вкладчика равен:

Д_р = S_i — 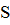= 16 923,1 – 20 000 = — 3076,9 руб. (реальный убыток).

Ответ.1) S = 21 000 руб., S_i = 16 153,2 руб., Д_р = — 3846,2 руб.; 2) S = 22 000 руб., S_i = 16923,1 руб., Д_р = — 3076,9 руб.

Источник

Задача №33. Расчёт реального дохода вкладчика с учётом инфляции

Вклад в сумме 35000 руб. положен в банк на год с ежемесячным исчислением сложных процентов; годовая ставка по вкладам 6%; уровень инфляции за месяц 10%.

Определить:

а) сумму вклада с процентами (FV),

б) индекс инфляции за 6 месяцев (I_n),

в) сумму вклада с процентами с точки зрения её покупательной способности (K_r),

г) реальный доход вкладчика с точки зрения покупательной способности (d).

Решение:

а) Сумму вклада рассчитаем по формуле наращения по сложным процентам:

FV – наращенная сумма вклада,

PV – настоящая стоимость денег,

n – срок операции,

m – число раз начисления процентов в году,

j – годовая (номинальная) ставка, выраженная десятичной дробью,

j/m – процентная ставка за период

FV = 35000 * (1 + 0,06 / 12) 12*1 = 37158,72 руб.

б) Индекс инфляции за 12 месяцев найдём по формуле:

I_n = (1 + 0,1) 12 = 3,1384.

в) Сумму вклада с процентами с точки зрения её покупательной способности (K _r ) найдём как отношение наращенной суммы вклада (FV) к индексу инфляции (I_n):

K_r = FV / I_n = 37158,72 / 3,1384 = 11839,91 руб.

г) Реальный доход вкладчика с точки зрения покупательной способности (d) вычислим так:

d = K_r – PV = 11839,91 – 35000 = – 23160,09 (реальный убыток).

Источник

Как правильно рассчитать реальную доходность с учетом инфляции

Многим известно, что инфляция негативно влияет на доходность инвестиции. Но не все умеют правильно рассчитывать реальную доходность с учетом инфляции.

Сначала определимся, что является доходностью.

Деньги обладают покупательной способностью. То есть в будущем на одну и ту же сумму сможете купить меньшее количество товаров и услуг. Покупательная способность денег определяется инфляцией.

Поэтому есть два варианта доходности:

• Номинальная доходность — рассчитанная без поправки на инфляцию.
• Реальная доходность — рассчитанная с поправкой на инфляцию, то есть с учетом будущей покупательной способности денег в сегодняшних ценах.

Как рассчитать реальную доходность?

Я заметил, что многие считают этот показатель по простой формуле:

Реальная доходность = Номинальная доходность — Инфляция

Но этот способ неточен. Причем, чем выше инфляция, тем точность все ниже.

Пример 1️⃣

Инфляция — 4% (сколько примерно она составила за 2020 год в России), а номинальная доходность — 15%.

По данной формуле реальная доходность составляет:

Это близко к истине, но не точно.

Пример 2️⃣

Инфляция — 120%, а номинальная доходность — 20%.

Сколько составит реальная доходность?

20% — 120% = -100%. Нет, такого быть не может.

Правильная формула для расчета:

Реальная доходность за год = (1 + номинальная доходность за год) / (1 + инфляция) — 1.

Давайте пересчитаем наши примеры:

Пример 1️⃣

Инфляция — 4%, а номинальная доходность — 15%

Реальная доходность за год = (1 + 15%) / (1 + 4%) — 1 = 10,6%.

А не 11%, как по первой формуле.

Пример 2️⃣

Инфляция — 120%, а номинальная доходность — 20%.

Реальная доходность за год = (1 + 20%) / (1 + 120%) — 1 = -45%.

А не -100%, как по первой формуле.

Надеюсь, понятно объяснил 🙂.

Считаете для себя реальную доходность?

Источник

Геометрическая разница, считаем реальную доходность

В прошлой публикации Где интуиция не срабатывает: считаем доходность мы рассказывали об алгебраической и геометрической суммах. Речь шла о том, как правильно считать доходность.

Когда мы употребляем термин доходность, то в большинстве случаев имеется ввиду номинальная доходность, то есть без учета инфляции. Как правило, инвестора интересует реальная доходность с учетом влияния инфляции.

Как и в прошлой статье начнем с простого примера. Если доходность депозита составила 18% годовых, а инфляция за тот же период — 11%, какова итоговая доходность?

Проверьте себя. Как бы вы посчитали результат?

Что случится, если вдруг инфляция в этот год взлетит до 118%?

Довольно часто в первом случае люди полагают, что Реальная доходность составила 7%:

Такое вычитание называется алгебраическим.

Работает ли алгебраическое вычитание во втором случае?

Может ли реальная доходность достигать -100% после учета инфляции? Это значило бы, что покупательная сила денег стала равной нулю. А если инфляция составила бы 120%, мы потеряли бы больше денег, чем у нас было? Вряд ли такой метод вычитания может быть правильным …

Как и раньше, помогает геометрическая разница:

При расчете процентные соотношения переводятся в десятичные дроби, хотя в EXCEL можно этого не делать. EXCEL умеет сам переводить из дробей в проценты и наоборот (см. прилагаемый файл).

Обобщаем

Если доходность составила R процентов, а инфляция равняется N, то реальная доходность вычисляется по формуле:

Всегда ли неправильно считать доходность через алгебраическую сумму?

В примере, когда номинальная доходность составила 18% а инфляция – 11%, можно заметить, что результаты алгебраического и геометрического вычитания довольно близки. Ошибка составит лишь 0,69%.

Действительно, иногда полезно пользоваться алгебраической разницей для получения приближенных результатов. Ошибка будет незначительной в тех случаях, когда инфляция и доходность не слишком сильно отличаются.

Тем не менее, когда рассматриваются доходности за несколько периодов или когда разница между номинальной доходностью и инфляцией значительна, величина ошибки возрастает.

Источник

Реальная доходность с учетом инфляции

Целью любого инвестирования является не только сохранение, но и приумножение денежных средств. Доходность – основной показатель эффективности инвестиционных вложений. Но в мире есть такое явление, как инфляция. И мы все знаем, что несколько лет назад на 100 тысяч рублей можно было купить больше товаров, чем сейчас. Инфляция может скорректировать доход инвестора и не в лучшую сторону. Поэтому для того, чтобы грамотно оценить свои инвестиции, надо обязательно учитывать влияние инфляции. Некоторые инвесторы делают это с помощью простого вычитания процента инфляции из номинальной доходности. Но этот метод не является точным. Для того, чтобы рассчитать реальную доходность с учетом инфляции надо воспользоваться соответствующей формулой.

Формула расчета доходности

Предположим, вы положили на депозит 1000 рублей при ставке 8% годовых. Инфляция – 5 процентов.

Через 10 лет эта тысяча превратится в 2159 рублей.

Рассчитана эта сумма так:

А теперь посмотрим, как за этот период вырастут потребительские цены:

Исходя из полученных значений, посчитаем реальную доходность. Для этого нужно разделить сумму депозита через 10 лет на значение инфляции:

Но для анализа удобней оперировать значениями в процентах.

Переводим полученную сумму в %:

(1324/1000)^1/10 -1 *100 = 2,8%.

Итак, мы выяснили, что реальная доходность с учетом инфляции при начальном депозите 1000 рублей составит 2,8%. А если бы мы посчитали ее по упрощенной формуле, то она бы составила 3% (8-5). Как видите, разница в размере дохода, рассчитанного двумя способам, есть.

Формулу расчета можно представить в таком виде:

Реальная доходность = (номинальная ставка доходности – уровень инфляции) / (1 + уровень инфляции)

Проверим на нашем примере насколько она верна:

(0,08 – 0,05) / (1 + 0,05) = 0,028

Умножаем на 100 и получаем реальную доходность 2,8%. Значение соответствует ранее произведенному расчету.

Могу предложить еще одну формулу для определения доходности, скорректированной на рост цен:

Real Rate of Return – это то, что нас интересует, то есть реальная доходность.

Nominal rate – это ставка доходности.

Inflation rate – уровень инфляции.

Проверяем эту формулу:

(1 + 0,08) / (1 + 0,05) -1 = 0,028 или 2,8%.

Какой из этих формул воспользоваться – решать вам. В любом случае реальная доходность с учетом инфляции, рассчитанная по каждой из них, будет правильной.

Источник