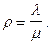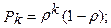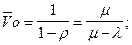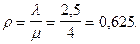Группа медиков собирается открыть частную медицинскую фирму если рынок будет благоприятным

Содержание

1. Дерево решений
Задачи с решениями
ЗАДАЧИ для самостоятельного решения. Методические указания для подготовки контрольной работы по операционному менеджменту

1. Дерево решений

Своевременная разработка и принятие правильного решения — главные задачи работы управленческого персонала любой организации. Непродуманное решение может дорого стоить компании. На практике результат одного решения заставляет нас принимать следующее решение и т. д. Когда нужно принять несколько решений в условиях неопределенности, когда каждое решение зависит от исхода предыдущего или исходов испытаний, то применяют схему, называемую деревом решений.

Дерево решений — это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.

Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами □, места появления исходов — кругами О,

возможные решения — пунктирными линиями—-, возможные исходы — сплошными линиями—-.

Задачи с решениями

З 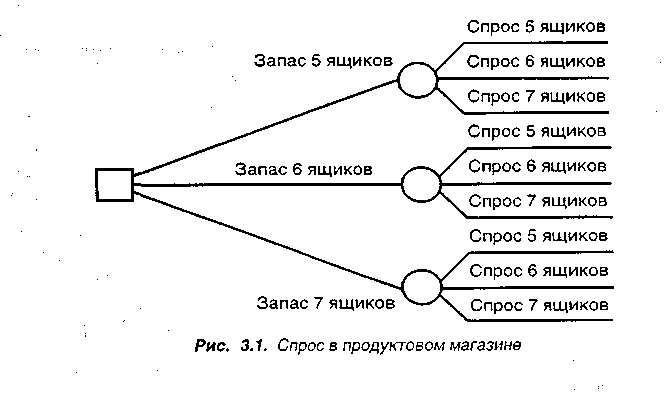адача 3.1 Ежедневный спрос на ящики с напитком в продуктовом магазине может быть пять, шесть или семь ящиков. Покажем дерево решений, которое иллюстрирует альтернативы запасов пяти, шести или семи ящиков.

Решение Дерево решений показано на рис. 3.1.

З 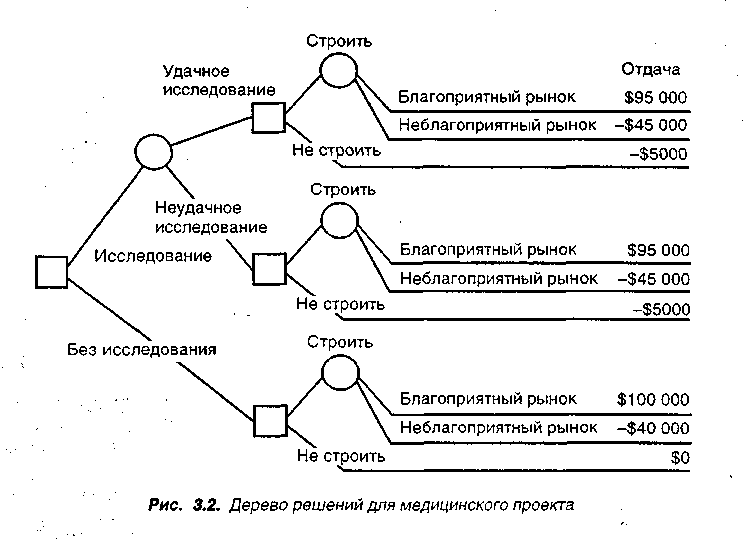адача 3.2 Группа медиков собирается открыть частную медицинскую фирму. Если рынок будет благоприятным, они будут иметь прибыль $100000. Если рынок неблагоприятный, они понесут потери $40000. Они также могут осуществить маркетинговое исследование, которое стоит $5000. Результаты исследования могут быть благоприятными или неблагоприятными. Медики хотят построить дерево решений и отразить на нем свою денежную отдачу. Дерево решений показано на рис. 3.2.

Решение В определении денежной отдачи для каждой ветви необходимо вычесть $5000 для тех ветвей дерева, где исследования проводились, т. е. для шести ветвей.

Далее, когда отдача определена для каждого исхода, или ветви дерева решений, следующий шаг состоит в установлении вероятностей каждого состояния внешней среды (см. рис. 3.3). Такие вероятности должен определить менеджер, принимающий решение на рынке. Тогда мы можем анализировать полностью дерево решений.

И 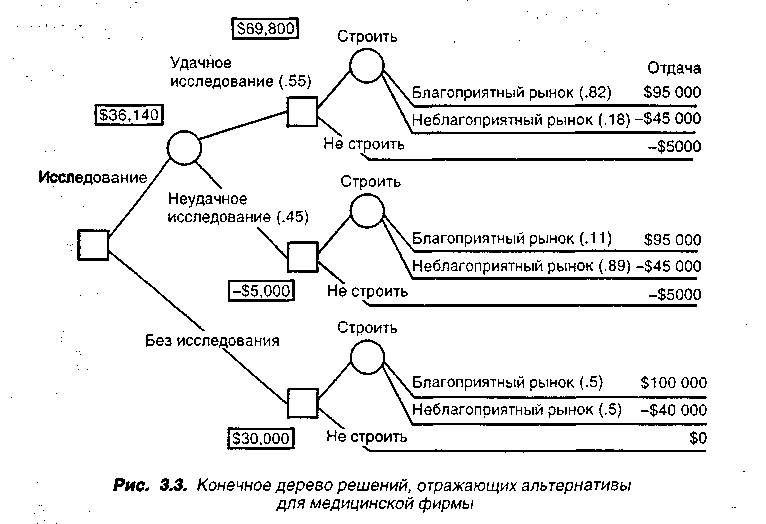з решения, отраженного на рис. 3.3, очевидно, что группа исследования рынка приглашается. Если исследование благоприятное, клиника должна быть построена, если нет, то клинику строить не будут. Решение с участием маркетинговой группы дает отдачу $36140, а без участия исследователей и при строительстве клиники приносит $30000. Тогда лучшее решение – проводить исследование и принимать решение на основе полученных рекомендаций.

Задача 3.3. Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) — максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов.

Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150) => оценка узла F: EMV(F) = 0,4X200 + 0,6х(-150) = -10. Это число мы пишем над узлом F.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения EMV((G) = 0): EMV(4) = max = max <-10, 0>= 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.

EMV(B) = 0,9*200 + 0,1*(-150) = 180 — 15 = 165

EMV(2) = max = max <165, 0>= 165 = EMV(B). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

EMV(.D) = 0,2*200 + 0,8*(-150) = 40 — 120 = -80.

E 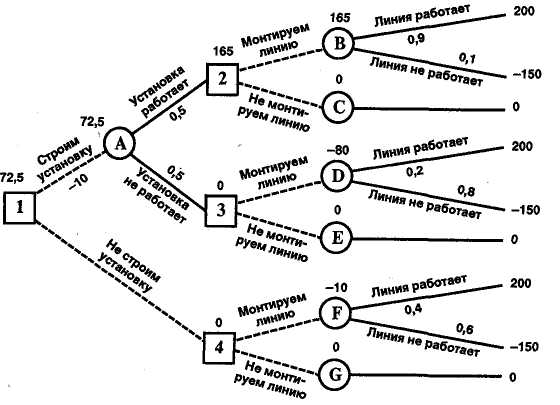MV(E) = 0.

EMV(3) = max = max <-80, 0>= 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

EMV(A) = 0,5*165 + 0,5*0 — 10 = 72,5.

Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.

Источник

ЗАДАЧИ для самостоятельного решения. Методические указания для подготовки контрольной работы по операционному менеджменту

Методические указания для подготовки контрольной работы по операционному менеджменту.

Контрольная работа выполняется по 5 вариантам, в соответствии с номерами по списку в журнале. Например, 1 вариант выбирают 1, 6, 11, 16, 21 студенты. Они решают задачи № 2, 7 из первого раздела (в разделе всего 10 задач, номера задач не по порядку), задачи № 1, 6 из второго раздела (в разделе всего 10 задач, номера задач не по порядку), задачи № 4, 10, 15, 20 из третьего раздела (в разделе всего 20 задач, номера задач не по порядку). В контрольной работе должен быть приведен порядок решения по действиям, со ссылками на использованные формулы.

Дерево решений

возможные решения — пунктирными линиями—-, возможные исходы — сплошными линиями—-.

ЗАДАЧИ с решениями

Задача 3.1 Ежедневный спрос на ящики с напитком в продуктовом магазине может быть пять, шесть или семь ящиков. Покажем дерево решений, которое иллюстрирует альтернативы запасов пяти, шести или семи ящиков.

Решение Дерево решений показано на рис. 3.1.

Задача 3.2 Группа медиков собирается открыть частную медицинскую фирму. Если рынок будет благоприятным, они будут иметь прибыль $100000. Если рынок неблагоприятный, они понесут потери $40000. Они также могут осуществить маркетинговое исследование, которое стоит $5000. Результаты исследования могут быть благоприятными или неблагоприятными. Медики хотят построить дерево решений и отразить на нем свою денежную отдачу. Дерево решений показано на рис. 3.2.

Из решения, отраженного на рис. 3.3, очевидно, что группа исследования рынка приглашается. Если исследование благоприятное, клиника должна быть построена, если нет, то клинику строить не будут. Решение с участием маркетинговой группы дает отдачу $36140, а без участия исследователей и при строительстве клиники приносит $30000. Тогда лучшее решение – проводить исследование и принимать решение на основе полученных рекомендаций.

Задача 3.3.Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) — максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов.

EMV(B) = 0,9*200 + 0,1*(-150) = 180 — 15 = 165

EMV(2) = max = max <165, 0>= 165 = EMV(B). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

EMV(.D) = 0,2*200 + 0,8*(-150) = 40 — 120 = -80.

EMV(E) = 0.

EMV(3) = max = max <-80, 0>= 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

EMV(A) = 0,5*165 + 0,5*0 — 10 = 72,5.

Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

ЗАДАЧИ для самостоятельного решения

Задача 3.2. ПК Женщина – предприниматель собирается открывать ресторан недалеко от университетского городка. По одному плану проект включает бар с продажей пива, другой план не включает бар. В том и другом случае ее шансы на успех будут .6 (и на провал .4). Ежегодный доход, включая бар, равен $325000. Без бара доход составит только $250000. Провал при наличии бара был бы оценен $70000, а без бара – $20000. Выберите вариант для предпринимателя, используя показатель денежной отдачи как критерий решения. Должен ли бизнес-план включать бар?

Задача 3.3 Предприятие является малым поставщиком химикатов и оборудования, используемых в фотографии. Один товар, поставляемый им, – это ВС-6. Менеджер обычно имеет запас 11, 12 или 13 ящиков ВС-6 на каждую неделю. За каждый проданный ящик полученная прибыль равна $35. Так как ВС-6 является реактивом с коротким сроком годности, то в случае непродажи его к концу недели менеджер должен его уничтожить. Он теряет $56 в каждом случае, когда что-то не продал в конце недели. Вероятность продажи 11 ящиков – .45, 12 ящиков – .35, и вероятность продажи 13 ящиков – .2. а) Что вы рекомендуете менеджеру делать? б) Если возможно добавить в ВС-6 ингредиенты, его стабилизирующие, как изменятся ваши рекомендации относительно запаса ВС-6?

Задача 3.4. ПК Малый производитель ряда продуктов из сыра определяет, сколько ящиков сыра производить каждый месяц. Вероятность, что спрос будет 6 ящиков, равна .1, семь – .3 и восемь – .5, девять – .1. Затраты на каждый ящик – $45, а цена – $95. В случае непродажи ящика к концу месяца он списывается как испорченный. Сколько ящиков сыра должно производиться каждый месяц?

Задача 3.5 Главный инженер предприятия решает, строить или не строить новую высокотехнологичную производственную линию. Если новое оборудование заработает, компания будет получать прибыль $200000. Если не заработает, то компания получит убыток $150000. Главный инженер считает, что шансы на неуспех нового процесса – 60 %.

Другое решение – проводить дополнительное исследование и тогда решать, пускать или не пускать новую линию. Такое исследование требует затрат $10000. Главный инженер считает, что шанс 50 : 50, что исследование даст благоприятный результат. Если оно успешно, то вероятность того, что оборудование будет работать, – 90 %. Если нет, то только 20 % составляют шанс, что оборудование будет работать. Перед лицом главного инженера – дилемма. Должен ли он проводить исследование и затем принимать решение? Помогите ему проанализировать эту проблему теории решений.

Задача 3.6 Президент компании решает, строить или нет промышленноепредприятие. Его решения сведены в следующую таблицу:

Варианты	Благоприятный рынок, $	Неблагоприятный рынок, –$
Строить большой завод
Строить малый завод
«Ничего не делать»
Вероятность	.4	.6

а) Постройте дерево решений. б) Определите лучшую стратегию, используя критерий EMV.

Задача 3.7 Промышленное предприятие получает выключатели от двух поставщиков. Качество выключателей от этих поставщиков показано ниже.

Процент дефектов	Вероятность для поставщика А	Вероятность для поставщика В
.70	.30
.20	.40
.10	.30

Объем поставки 10000 выключателей. Неисправный выключатель может быть отремонтирован за $0.50. Хотя качество у поставщика В ниже, но он просит за 10000 выключателей на $37 меньше, чем поставщик А. а) Нарисуйте дерево решений. б) Какой поставщик будет использоваться?

Задача 3.12 Предприниматель в задаче 3.11 сделал такой анализ решения о своем магазине велосипедов. Если он открывает большой магазин, то будет зарабатывать $60000, если рынок благоприятный, но будет нести потери $40000, если рынок неблагоприятный. Маленький магазин будет приносить $30000 прибыли при благоприятном рынке и $10000 потерь, если рынок неблагоприятный. В настоящее время предприниматель считает, что существует шанс 50 : 50, что рынок будет благоприятным. Его профессор по маркетингу назначил цену $5000 за маркетинговое исследование. Он оценил, что существует вероятность .6 того, что исследование рынка будет успешным. Вероятность .9 определяет благоприятный рынок при успешном результате исследования. Кроме того, только .12 составляет вероятность благоприятного рынка, если результаты исследования рынка неблагоприятные. Постройте дерево решений задачи 3.12, которое поможет предпринимателю решить, что ему делать.

Задача 3.13 Предприниматель не знает, что ему делать: он может открыть большой отдел проката скутеров или маленький отдел в своем магазине; он может также собирать информацию, результаты будут показывать благоприятный или неблагоприятный рынок, но это будет стоить ему $3000 за информацию. Предприниматель считает, что имеется шанс 50 : 50, что информация будет благоприятной. Если рынок проката благоприятный, предприниматель будет получать доход $15000 в большой отделе или $5000 в маленьком. При неблагоприятном рынке проката скутеров убыток составит $20000 при большом отделе и $10000 при маленьком отделе. Благоприятный отчет при изучении рынка повышает вероятность существования благоприятного рынка до .9. Кроме того, неблагоприятный рыночный отчет понижает вероятность благоприятного рынка проката до .4. Что вы посоветуете делать предпринимателю?

Задача 3.14. Президент электронной фирмы имеет два решения для ее новой линии катодных лучевых трубок (CRT) для компьютерных рабочих станций. Продажи CRT в течение жизненного цикла прогнозируются в размере 100000 штук.

Решение А имеет вероятность .90 производства 59 хороших CRT из 100 и вероятность .10 производства 64 хороших CRT из 100. Это решение будет требовать затрат $1000000.

Решение В имеет вероятность .80 производства 64 хороших изделий из 100 и вероятность .20 производства 59 хороших изделий из 100. Это решение требует затрат в $1350000.

Хорошая или плохая, каждая CRT будет иметь себестоимость $75. Каждая хорошая CRT будет продана за $150. Плохие CRT уничтожаются и не дают никакого дохода.

Задача 3.15. Используя данные задачи 3.14. , найдем решение в случае, если производитель может изменить производство 59 из 100 единиц CRT с использованием специальных экранов, увеличивающих затраты на $50 на каждую CRT. Этот производственный процесс будет успешным только для пяти изделий из 100.

Раздел 2 Теория очередей

Модель, иллюстрируемая одноканальной однофазной системой с пуассоновым распределением появления заявок и экспоненциальным временем обслуживания – это модель А; модель В – многоканальный эквивалент модели А; модель С характеризуется постоянным временем обслуживания; модель D – с ограниченным размером источника появления заявок.

Все четыре модели связаны с пуассоновым распределением заявок, дисциплиной обслуживания «первым пришел, первым ушел» и с однофазным сервисом.

Типичными операционными характеристиками рассматривают среднее время ожидания в очереди и в системе, среднее число заявок в очереди и в системе, время простоя и коэффициент использования системы.

Интенсивность нагрузки систем ,

Величина представляет собой долю времени занятости канала обслуживанием требований и изменяется в пределах = 0 — 1. При = 0 канал совершенно не загружен ( =0), при =1 ( ) канал загружен полностью.

— вероятность того, что в системе есть требование, равна ;

вероятность того, что в системе нет требований (k=0), представляет собой вероятность противоположного события и равна ;

вероятность того, что в системе находится больше одного требования (т.е. вероятность образования очереди), равна

вероятность того, что в системе более п требований, равна

— вероятность того, что в системе находится k требований (в очереди или в канале обслуживания), равна

— среднее число требований, находящихся в системе, равно

— среднее число требований в очереди для всего периода функционирования системы равно

среднее число требований в очереди для того времени, когда очередь существует ( ), равно

— среднее время ожидания требованием обслуживания равно

среднее время пребывания заявки в системе равно

С помощью данных зависимостей можно рассчитывать основные показатели, характеризующие качество процесса обслуживания, т.е. решать задачи оценки.

Для решения задач оптимизации необходимо сформулировать критерий. Поскольку внешние условия функционирования считаются заданными характером и интенсивностью потока заявок, цель оптимизации состоит в том, чтобы выбрать такую систему обслуживания, которая позволила бы свести потери от ожидания в очереди и простоя канала обслуживания до минимума. Эта цель достигается главным образом выбором оптимальной пропускной способности канала.

Задачу можно сформулировать как обратную задачу, которая состоит в выборе лучшей пропускной способности канала обслуживания. Лучшей будем считать такую пропускную способность, которая при заданном потоке заявок обеспечит минимальные потери от нахождения заявок в очереди и затрат на содержание канала обслуживания.

Потери от нахождения в системе одной заявки в единицу времени С1, а затраты на содержание единицы пропускной способности канала обслуживания С2..

Для многоканальных систем обслуживания основными параметрами являются:

— среднее число требований в очереди ( );

— среднее число требований в системе ( ;

— среднее время ожидания обслуживания одного требования ( ;

— среднее время пребывания требования в системе (

— вероятность образования очереди (вероятность того, что в системе с S каналами находится требований).

Эти характеристики позволяют не только определять основные показатели многоканальных систем обслуживания, но и решать задачи оптимизации их пропускной способности. Для нахождения оптимального числа каналов в системе можно воспользоваться целевой функцией следующего вида:

где L — потери от ожидания требованиями обслуживания и от простоев каналов обслуживания в единицу времени;

С — убытки от ожидания одной заявкой обслуживания в единицу времени;

— среднее число заявок, ожидающих обслуживания;

С — убытки от простоя канала обслуживания в единицу времени;

— среднее число незанятых каналов.

ЗАДАЧИ С РЕШЕНИЯМИ

Задача 5.1.0Согласно утвержденному графику доставка материалов на строительную площадку должна осуществляться в течение 8-часового рабочего дня на 20 автомобилях. Бригада грузчиков обеспечивает разгрузку материалов с одного автомобиля за 15 мин. Определить возможные потери из-за простоя автомобилей в связи с неравномерным прибытием их на строительную площадку, если потери от простоя одного автомобиля в час составляют 5 руб.

Решение: 1. Средняя плотность потока автомобилей за рабочий день

автомобиля в час.

2. Бригада грузчиков может разгрузить в среднем 4 авт. в час.

3. Интенсивность загрузки бригады грузчиков

4. Среднее время простоя одного автомобиля в ожидании разгрузки

часа.

5. Простой всех автомобилей за рабочий день 20х0,42 = 8,4 маш.-час.

6. Потери вследствие простоя автомобилей 8,4х5 = 42 руб.

Задача 5.1.1 На ремонтном предприятии для проверки качества ремонта двигателей необходимо установить аппаратуру контроля. Рассчитать оптимальную пропускную способность аппаратуры, если потери от нахождения в системе контроля C1=60 руб., затраты на закупку и текущее содержание единицы пропускной способности системы контроля С2=130 руб. В среднем каждый час на контроль поступает 1,2 готовых двигателя.

Решение. Целевая функция имеет вид

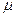
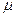
В первом слагаемом целевой функции характеристика пропускной способности стоит в знаменателе, а во втором в числителе, следовательно, они по-разному влияют на потери L. Подбирая , можно найти такое его значение, при котором L будет минимальным. Расчет целесообразно вести по следующему алгоритму.

1. Задать значения 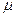несколько больше, чем , чтобы не было бесконечной очереди.

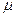
2. При зад. значении и принятом рассчитать интенсивность нагрузки системы .

3. Рассчитать среднее время пребывания двигателя в системе контроля .

4. Рассчитать потери от нахождения в системе обслуживания С1 .

5. Рассчитать затраты на создание и содержание системы контроля С2 .

6. Рассчитать потери

7. Операции 1-6 повторить, увеличив 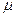, например, на 0,1.

8. Сравнить полученное значение L с ранее рассчитанным. Если потери L уменьшились, то необходимо продолжать расчеты по пп. 2-6.

При некоторых значениях 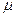потери начнут увеличиваться. Минимальное значение потерь укажет на оптимальную пропускную способность системы контроля двигателей. Результаты расчетов по данному алгоритму приведены в табл. 1.

			C1	C2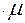
1,3	0,92
1,4	0,86
1,5	0,8	3,33
1.6	0,75	2,5
1,7	0,71	2,0
1,8	0,67	1,667
1,9	0,63	1,43	85,7	332,7
2,0	0,6	1,25
2,1	0,57	1,11	66,7	339,7

Анализ данных, приведенных в табл.1, показывает:

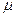
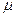
— с ростом пропускной способности с 1,3 до 2,1 потери от ожидания контроля падают почти в 10 раз (с 600 до 66,7 руб.). В то же время затраты на создание и содержание системы контроля увеличились пропорционально со 169 до 273 руб.;

— минимальные потери 332,7 руб. будут при 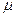=1,9. Следовательно, необходимо создавать систему контроля двигателей именно с пропускной способностью 1,9 двигателя в час. Система контроля с большей или меньшей пропускной способностью приведет к росту потерь либо за счет увеличения времени ожидания (при меньшей пропускной способности, чем 1,9), либо за счет простоя системы (при большей пропускной способности);

— вытекающие из таблицы выводы опровергают весьма распространенное заблуждение, что нужно стремиться к =1. В этом случае резко возрастают потери от ожидания обслуживания. При увеличении интенсивности нагрузки в 1,5 раза, т. е. с 0,63 для оптимального варианта до 0,92, потери возросли более чем в 2 раза (с 332,7 до 769 руб.). Для принятых исходных данных оптимальной будет загрузка системы контроля лишь на 63%. Такой вариант, несмотря на внешнюю парадоксальность, является наиболее экономичным.

Если такого рода анализ для лица, принимающего решение, не представляет интереса, то оптимальное значение 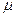можно найти проще, без построения вспомогательной таблицы.

Для этого необходимо взять формулу для оптимального значения *: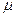

В полученную формулу подставим исходные данные примера 6.4 и рассчитаем оптимальную пропускную способность *: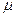

Рассчитанная пропускная способность соответствует результату, полученному в примере ( = 1,9).

Задача 5.1.2Найти оптимальное количество технологических линий авторемонтного завода по критерию минимума потерь в сутки исходя из следующих условий: интенсивность потока автомобилей в ремонт — 2 машины в смену;

— средняя длительность ремонта одного автомобиля – одна смена;

— потери от ожидания одним автомобилем ремонта — C =500 руб. за смену;

— убытки от простоя одной технологической линии -С =350 руб. за смену.

— среднее число автомобилей , ожидающих ремонта, для различных количеств технологических линий S приведены в таблице 7.5.

Решение. 1.Обозначим количество технологических линий через S. Тогда количество незанятых каналов будет (приведены в табл.).

2. Рассчитаем интенсивность нагрузки системы

3. Результаты расчетов сводятся в таблицу 2.

S	C	C	C
0,888
0,1739
0,04
0,0093

Из табл.2 следует, что минимальные потери будут при четырех технологических линиях. Следовательно, оптимальным является S*= 4.

Задача 5.1 Компания нанимает ежегодно одного рабочего, чьей обязанностью является погрузка кирпича на грузовики компании. В среднем проходит 24 грузовика в день, или три грузовика в час, которые появляются согласно распределению Пуассона. Рабочий загружает их по правилу четыре грузовика в час, время обслуживания подчиняется экспоненциальному закону.

Полагают, что второй грузчик существенно повысит производительность в фирме. Менеджеры рассчитывают, что два грузчика будут работать по тому же правилу: четыре грузовика в час на одного и восемь грузовиков в час на двоих. Проанализируйте эффект в очереди от такого изменения и сравните с результатом, найденным для одного рабочего. Какова вероятность того, что будет больше чем три грузовика загружаться или ожидать в очереди?

Решение

Характеристики системы	Количество грузчиков:
один	два
Правило прибытия грузовиков l	3 / ч	3 / ч
Правило погрузки т	4 / ч	8 / ч
Среднее число грузовиков в системе Ls	3 грузовика	.6 грузовиков
Среднее время в системе Ws	1ч	.2ч
Среднее число грузовиков в очереди Lg	2.25 грузовика	.225 грузовиков
Среднее время в очереди Wq	3/4 ч	.075 ч
Коэффициент использования р	.75	.375
Вероятность нуля грузовиков в системе Р₀	.25	.625

Вероятность более, чем k грузовиков в системе

k	Вероятность n > k
Один грузчик	Два грузчика
.75	.375
.56	.141
.42	.053
.32	.020

Эти результаты показывают, что когда только один грузчик нанят, грузовик в среднем должен ждать 3/4 часа прежде, чем его погрузят; более того, в среднем 2.25 грузовика стоят в очереди на погрузку. Эта ситуация может быть недопустима для службы менеджмента. Возможно уменьшение размера очереди за счет добавления второго грузчика.

Задача 5.2 Водители грузовиков, работающие в компании (смотри задачу 5.1) получают $10 в час в среднем. Грузчики получают около $6 в час. Водители грузовиков, ожидая в очереди, получают зарплату, но бесполезно проводят это время. Что будет с часовыми затратами, если фирма наймет двух грузчиков вместо одного?

Используя данные задачи 5.1, мы узнаем, что среднее количество грузовиков в системе – 3, когда работает только один грузчик, и .6, когда их двое.

Решение

Затраты	Количество грузчиков:
один	два
Затраты за время незанятости водителей	(3)($10) = $30	$6 = (.6)($10)
[(среднее число грузовиков) х (часовая зарплата)]
Затраты на погрузку	$6	$12 = (2)($6)
Общие затраты в час	$36	$18

Фирма экономит $18 в час, нанимая второго грузчика.

Задача 5.3 Компания собирается строить вторую платформу, чтобы ускорить процесс погрузки кирпичей на грузовики. Эта система, как думают менеджеры, будет более эффективна, чем просто наем другого грузчика в помощь тому, кто работает на первой платформе (как было сказано в задаче 5.1).

Также рассчитывают, что рабочие на каждой платформе будут способны нагружать четыре грузовика в час каждый и что грузовики будут появляться в очереди по правилу три машины в час. Применив затем соответствующие уравнения, находят параметры очереди в новых операционных условиях. Является ли новый подход более быстрым, чем другие два из рассмотренных?

Решение

Среднее число грузовиков в системе и среднее время ожидания в системе больше, чем когда два рабочих работают на погрузке на одной платформе. Следовательно, вторую платформу строить не рекомендуется.

Задача 5.4 Госпиталь имеет пять коек, которые предназначены для срочных больных, доставляемых в кардиологическое отделение. Две регистрационные сестры работают на приеме больных в отделении.

В среднем каждые два часа (в соответствии с распределением Пуассона) в отделении появляется пациент. Сестра тратит в среднем 30 минут на осмотр и регистрацию пациента (время осмотра подчиняется экспоненциальному распределению). Если одновременно могут появиться пять пациентов, требующих обслуживания, встают два важных вопроса: каково среднее число пациентов в очереди к сестре и каково среднее время ожидания в очереди к каждой сестре?

Решение

N =5 пациентов. М = 2 сестры. Т = 30 мин. U = 120 мин.

Х = Т / (Т + U) = 30 / (30 + 120) = .20.

Для X = .20 и М = 2 F = .976.

Н = Среднее число пациентов в очереди = FNX =

= (.976) (5) (.20) = .98 = один пациент;

W = Среднее время ожидания в очереди = [T (1 – F)] / XF =

= [30 (1 – .976)] / [(20.) (.976)] = 3.69 мин.

Источник