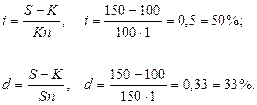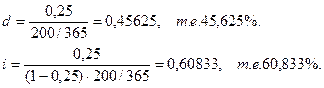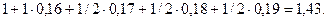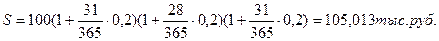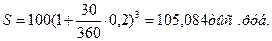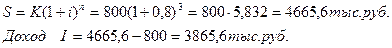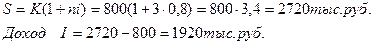Доходность операции наращения простыми процентами

Формулы доходности финансовых операций

Если в формулах наращения по процентной и учетной ставке принять срок n = 1 году, то получим, что

.

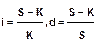
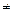
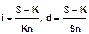
Если n1 году, .

Эти формулы принято называть формулами доходности или эффективности по простой ставке процентов и учетной ставке соответственно.

Предприятие получило кредит на 1 год в размере 100 млн. с условием возврата 150 млн.

Найти доходность операции для кредитора в виде процентной и дисконтной (учетной) ставок.

К = 100 млн., S = 150 млн., n = 1 год. I = ?, d = ?

Решение:

Дисконтная ставка всегда меньше процентной, ибо она учитывает время более жестко.

Иногда размер дисконта в контрактах фиксируется за весь срок ссуды в виде доли (или процента) от суммы погасительного платежа. Таким образом, уровень процентной ставки задается в неявном виде. Выведем формулы, с помощью которых можно вычислить значения этих ставок.

Пусть S- размер погасительного платежа (сумма ссуды к концу срока),

d_n – доля этого платежа, определяющая величину дисконта за весь срок ссуды.

К = S(1 – d_n) – реально выдаваемая ссуда в момент заключения договора.

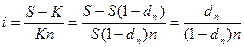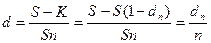Задача 7.

Кредитор и заемщик договорились, что из суммы кредита, выданного на 200 дней, сразу удерживается дисконт в размере 25% указанной суммы. Требуется определить цену кредита в виде простой годовой учетной ставки d и годовой простой ставки i. Год полагать равным 365 дней.

Простые переменные ставки

В кредитных соглашениях иногда предусматриваются изменяющиеся во времени процентные ставки.

Если i₁, i₂,… i_k – последовательные во времени простые ставки,

а n_1, n_2,… n_k – периоды, в течение которых применяются соответствующие ставки, тогда наращенная сумма определяется следующим образом:

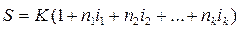Контракт предусматривает следующий порядок начисления процентов: первый год – ставка 16%, в каждый последующем полугодии ставка повышается на 1%. Определить множитель наращения за 2,5 года.

Общий срок начисления процентов 1+1/2+1/2+1/2=2,5 года.

Множитель наращения =

Иначе, за 2,5 года начальный капитал увеличился в 1,43 раза.

Реинвестирование

В практике при реинвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока, т.е. к реинвестированию средств, полученных на каждом этапе наращения. (Напоминает наращение по сложным процентам, но только напоминает!)

В этом случае наращенная сумма для всего срока составит:

(14) k – количество реинвестиций.

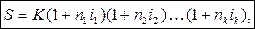
Если периоды начисления и ставки не изменяются во времени, то формула реинвестирования примет вид:

, k – количество реинвестиций.

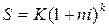
Задача 9.

Сумму в 100 тысяч рублей положили 1 января на месячный депозит под 20% годовых. Каковой будет наращенная сумма, если операция повторяется 3 раза? Расчет сделать по точным и банковским процентам.

По условию задачи депозит в 100 тысяч рублей реинвестируется трижды по простым процентам.

По точным процентам:

(Помните, что в январе 31 день, в феврале – 28 дней, в марте – 31 день!)

По банковским процентам при условии, что в каждом месяце по 30 дней:

Модуль 2. Сложные проценты

Наращение по сложным процентам

В среднесрочных и долгосрочных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, то для наращения используются сложные проценты.

Сложные проценты отличаются от простых процентов базой начисления. Если в простых процентах она остается постоянной на весь срок начисления, то в сложных при каждом начислении процентные деньги присоединяются к первоначальной базе. Говорят, идет капитализация процентов.

Формула наращения по сложным процентам, если проценты начисляются один раз в году, имеет вид

(1) , где i — годовая (номинальная) процентная ставка, n — число лет начисления,

— множитель наращения по сложным процентам.

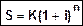
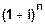
Задача 1.

Сумма, равная 800 тыс. руб., инвестируется на 3 года под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

2. Простые проценты:

За 3 года 800 тыс. руб. увеличились в 5,832 раза по сложным процентам и только в 3,4 раза по простым процентам.

Задача 2.

Сумма, равная 800 тыс. руб., инвестируется на 3 месяца под 80% годовых. Найти наращенную сумму и сумму процентов за этот срок, используя простые и сложные проценты.

Источник

ВАЛЮТА=> РУБЛИ => РУБЛИ => ВАЛЮТА.

Операция состоит из трех этапов: обмена валюты на рубли, наращения рублевой суммы, обратное конвертирование рублевой суммы в исходную валюту. Наращенная сумма, получаемая в конце операции в валюте, составит

Как видим, три этапа операции нашли свое отражение в этой формуле в виде трех сомножителей.

Множитель наращения с учетом двойного конвертирования равен

(2)

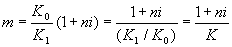
где k = K ₁ / K ₀ — темп роста обменного курса за срок операции. Из (2) следует, что множитель наращения т связан линейной зависимостью со ставкой i и обратной с обменным курсом в конце операции K ₁ (или с темпом роста обменного курса k ).

Исследуем зависимость общей доходности операции с двойной конверсией от соотношения конечного и начального курсов обмена k.

Простая годовая ставка процентов, характеризующая доходность операции, равна

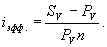
Подставим в эту формулу выражение для S_v

(3)

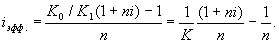
Из (3) следует, что с увеличением k доходность i_эфф падает по гиперболе с асимптотой 1/п. При k =1 доходность операции равна рублевой ставке, т.е. i_эфф = i . При k > 1 i _эфф i , а при k i _эфф >i. При некотором критическом значении k , которое обозначим как k * , доходность операции равна нулю. Из равенства i_эфф = 0 находим

Таким образом, если ожидаемые величины k или К * ₁ превышают свои критические значения, то операция убыточна ( i _эфф 0 ).

Определим максимально допустимое значение курса обмена в конце операции K ₁ , при котором эффективность будет равна существующей ставке по депозитам в валюте, и применение двойного конвертирования не дает никакой дополнительной выгоды. Для этого приравняем множители наращения для двух альтернативных операций

Из равенства следует, что

Таким образом, депозит валюты через конверсию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max K ₁ .

РУБЛИ => ВАЛЮТА => ВАЛЮТА ==> РУБЛИ.

Это операция с двойной конверсией, когда исходная и конечная суммы в рублях. В этом случае трем этапам операции соответствуют три сомножителя для наращенной суммы

(8)

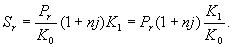
Проведем анализ эффективности этой операции и определим критические точки.

Доходность операции в целом определяется по формуле

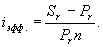
Отсюда, подставив выражение для S_r , получим

(9)

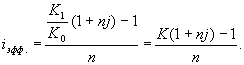
Найдем критическое значение k * , при которых i _эфф = 0:

Таким образом, если ожидаемые величины k или K ₁ меньше своих критических значений, то операция убыточна ( i _эфф 0 ).

Минимально допустимая величина k (темпа роста валютного курса за весь срок операции), обеспечивающая такую же доходность, что и прямой вклад в рублях, определяется путем приравнивания множителей наращения для альтернативных операций (или из равенства i _эфф = i ).

Таким образом, депозит рублевых сумм через конверсию в валюту выгоднее рублевого депозита, если обменный курс в конце операции ожидается больше min K₁.

Рассмотрим вариант совмещения конверсии валюты и наращение сложных процентов.

ВАЛЮТА => РУБЛИ => РУБЛИ =>ВАЛЮТА.

Три этапа операции запишем в одной формуле для наращенной суммы

где i — ставка сложных процентов.

где k = K ₁ / K ₀ — темп роста валютного курса за период операции.

Определим доходность операции в виде годовой ставки сложных процентов i _э . Из формулы наращения по сложным процентам

находим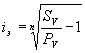

Подставив в эту формулу значение S_v , получим

(14)

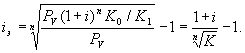
Из этого выражения следует, что с увеличением темпа роста k эффективность i _э падает.

Анализ показывает, что при k = 1 i _э = i , при k >1 i _э i , а при k i _э > i . Критическое значение k, при котором эффективность операции равна нулю, определяется как

что означает равенство среднегодового темпа роста курса валюты годовому темпу наращения по рублевой ставке .

Таким образом, если ожидаемые величины k или K ₁ больше своих критических значений, то рассматриваемая операция с двойной конверсией убыточна ( i _э

Максимально допустимое значение k , при котором доходность one рации будет равна доходности при прямом инвестировании валютных средств по ставке j , находится из равенства соответствующих множителей наращения:

k_max = (1+ i) n / (1+ j) n max K₁ = K₀ (1+ i) n / (1+ j) n . (16)

Таким образом, депозит валюты через конверсию в рубли выгоднее валютного депозита, если обменный курс в конце операции ожидается меньше max K ₁ .

Имеется сумма в долларах, которую предполагается разместить на полугодовой депозит. Обменный курс в начале операции 34 р. за доллар, в конце операции предполагается 35 р. Годовая ставка простых процентов по рублевым депозитам 12%, по валютным 5%.

Как выгоднее разместить вклад, как валютный или через конверсию в рублях?

При двойной конверсии: доллар Þ рубли Þ рубли Þ доллар расчет производим по формуле (3) с учетом того, что k = K ₁ / K ₀,, где

k – темп роста обменного курса за срок операции,

K ₀ – курс обмена в начале операции,

K ₁ – курс обмена в конце операции.

i _э = [ (1 + 0,5 × 0,12) / 1,029 × 0,5 ] — 1 / 0,5 = 0,06.

По условию задачи, доходность валютного депозита 5%, доходность операции с двойной конверсией 6%. Следовательно, выгоднее разместить вклад рублевый.

Пример 2. В обменном пункте установлена следующая котировка американского доллара к рублю; покупка – 29 руб., продажа 29,8 руб.

а) сколько рублей будет получено при обмене 350 долларов;

б) какое количество американских долларов можно приобрести на 4500 евро.

а) Для перевода суммы в иностранной валюте в эквивалентную ей сумму в национальной валюте необходимо умножить ее на курс покупки:

350 × 29=10150 руб.

б) Для перевода суммы в национальной валюте в эквивалентную ей сумму в иностранной валюте необходимо ее разделить на курс продажи:

доллар

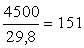
Пример 3. В банке установлена следующая котировка валют:

Источник