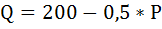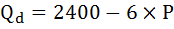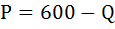Для стимулирования сбыта своей продукции фирма ibs объявила

Эластичность

Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу

Фирма имеет кривую спроса:

Зная, что P=100 , определить изменение дохода при увеличении проданной продукции на одну единицу.

Задача №2. Коэффициент точечной эластичности

Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.

а) Как изменилась выручка фирмы?

б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.

Задача №3. Эластичность спроса по цене

Функция задана уравнением

а) Выведите формулу эластичности этого спроса.

б) При какой цене эластичность спроса по цене составит – 0,5?

в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?

Задача №4. Функция суммарного спроса

а) Определить функцию суммарного спроса на основании данных об индивидуальном спросе:

Q(1) = 100 – 5 P при P≤ 20 и 0 при Р > 20 ,

Q(2) = 50 – 8 P при P≤ 10 и 0 при Р > 10 ,

Q(3) = 56 – 4 P при P≤ 14 и 0 при Р > 14 .

б) Найти эластичность спроса в точке P = 12 .

Задача №5. Функция суммарного спроса

Известны данные об индивидуальном спросе:

Q(1) = 80 – 8 P при P ≤ 10 и 0 при Р > 10 ,

Q(2) = 50 – 10 P при P ≤ 5 и 0 при Р > 5 ,

Q(3) = 32 – 4 P при P ≤ 8 и 0 при Р > 8 .

а) Выведите уравнение кривой спроса аналитически.

б) Получите формулу эластичности по абсолютной величине в зависимости от цены.

Источник

Формула эластичности

Задача №1. Определение изменения дохода при увеличении проданной продукции на одну единицу

Фирма имеет кривую спроса:

Зная, что P=100 , определить изменение дохода при увеличении проданной продукции на одну единицу.

Задача №2. Коэффициент точечной эластичности

Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.

а) Как изменилась выручка фирмы?

б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.

Задача №3. Эластичность спроса по цене

Функция задана уравнением

а) Выведите формулу эластичности этого спроса.

б) При какой цене эластичность спроса по цене составит – 0,5?

в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?

Задача №5. Функция суммарного спроса

Известны данные об индивидуальном спросе:

Q(1) = 80 – 8 P при P ≤ 10 и 0 при Р > 10 ,

Q(2) = 50 – 10 P при P ≤ 5 и 0 при Р > 5 ,

Q(3) = 32 – 4 P при P ≤ 8 и 0 при Р > 8 .

а) Выведите уравнение кривой спроса аналитически.

б) Получите формулу эластичности по абсолютной величине в зависимости от цены.

Задача №6. Расчёт дуговой эластичности

Является ли спрос на товар эластичным, если известно:

Источник

Выручка

Задача №2. Коэффициент точечной эластичности

Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.

а) Как изменилась выручка фирмы?

б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.

Задача №11. Расчёт выручки

Кривая спроса на продукцию монополиста описывается уравнением

Монополист установил такую цену на товар, при которой эластичность спроса на него равна (-2). Определить величину выручки монополиста.

Задача №18. Расчёт добавленной стоимости

Фирма по производству автомобилей приобрела у сталелитейной фирмы прокат на сумму 1500 тыс. дол., покрышки у шинного завода на сумму 600 тыс. дол., комплектующие у различных фирм на сумму 1200 тыс. дол., выплатила зарплату своим рабочим в размере 1000 тыс. дол., потратила 300 тыс. дол. на замену изношенного оборудования и продала изготовленные 200 автомобилей по 30 тыс. дол. каждый, при этом прибыль фирмы составила 400 тыс. дол. Определите величину добавленной стоимости автомобильной фирмы.

Задача №19. Расчёт чистой прибыли

Определить размер прибыли, остающейся в распоряжении предприятия, если реализовано 1030 изделий А по свободной оптовой цене 300 руб. за штуку, 580 изделий Б по свободной оптовой цене 210 руб. за штуку (НДС 18 %), оказано услуг на сумму 24 500 руб.

Себестоимость реализованной продукции 300 тыс. руб., затраты на осуществление услуг составили 17 000 руб.

Прибыль от участия в совместной деятельности других предприятий – 30 тыс. руб.

Реализовано ненужное оборудование на сумму 55 тыс. руб.

Предприятием уплачены штраф за нарушение условий договора поставки – 10 тыс. руб.

Ставка налога на прибыль составляет 20%.

Распределить прибыль, остающуюся в распоряжении предприятия в фонд потребления и фонд накопления, самостоятельно.

Задача №25. Вычисление перекрёстной эластичности спроса

Вычислить перекрёстную эластичность спроса на товар А, если цена дополняющего товара увеличилась на 5%, а выручка от реализации товара А по прежней цене при этом изменилась на 2%.

Два способа расчёта

Рента

Совершенная конкуренция

Совершенная конкуренция

Темп роста

Средняя арифметическая

Издержки

Задача №26. Оценка доходности инвестиций в предприятие

Вам предложили за 2,5 млрд. руб. купить предприятие, которое сейчас ежегодно реализует 100 тыс. изделий по цене 10 тыс. руб./шт. и даёт прибыли 200 млн. руб. ежегодно.

Деньги у Вас есть. В настоящее время они размещены в государственные ценные бумаги, по которым вы получаете 2,41% в квартал.

1). Что Вы скажите по поводу этого предложения.

2). У Вас есть идея, как, вложив в это предприятие ещё 1 млрд. руб., добиться увеличения объёма продаж на 15% в первый год, ещё на 10% во второй и ещё на 10% в третий.

Затраты при этом возрастают в первый год на 10 % и на 5% во второй (начиная с третьего года объём продаж и затраты останутся постоянными).

Повлияет ли эта возможность на Ваше решение?

3). Предположим, указанный в пункте 2 проект уже кем-то осуществлён.

Сколько теперь вы будете готовы дать за это предприятие.

Задача №29. Владелец хочет увеличить выручку

Владелец видеозала хочет увеличить выручку от продажи входных билетов. Чтобы достичь цели, он увеличил цену билетов. При каких условиях он добился бы желаемого? При каких условиях его выручка уменьшится?

Задача №41. Расчёт изменения товарооборота в относительном и абсолютном выражении

Выручка от продажи мяса и мясопродуктов на рынке в январе превысила выручку от продажи рыбы и рыбопродуктов в 2 раза. В феврале продажа мяса и мясопродуктов возросла на 15%, рыбы и рыбопродуктов – на 20%.

Определите:

1) на сколько процентов в среднем возросла продажа двух видов продукции вместе:

2) абсолютный прирост товарооборота по обоим видам продукции вместе вследствие среднего увеличения объема их продаж в натуральном выражении, если в январе за мясо и мясопродукты продавцами выручено 24 тыс. руб.

Задача №74. Расчёт бухгалтерской и экономической прибыли

Учитель географии, получавший в конце года после всех вычетов (в том числе и подоходного налога) 18 тыс. р. в год, в новом году решил открыть собственный магазин. Его стартовый капитал составляет 25 тыс. р. Он рассчитывает получить выручку, равную 170 тыс. р.

Для реализации этого проекта ему нужно:

1. оплатить в начале года арендную плату в размере 40 тыс. р. за помещение магазина на год вперёд;

2. в начале года выполнить ремонтные работы в арендуемом помещении стоимостью 20 тыс. р.;

3. нанять трёх работников с оплатой по 15 тыс. р. в год каждому, причём 5 тыс. р. выплатить в начале года в качестве аванса, а остальные 10 тыс. р. заплатить в конце года из выручки;

4. занять в банке недостающую для покрытия расходов сумму денег сроком на год;

5. оставить труд учителя и целиком сосредоточиться на предпринимательской деятельности.

Иных затрат у него нет. Банковский процент по депозитам равен 40%, а по кредитам – 50%.

Определить:

а) Величину бухгалтерской и экономической прибыли за год (в тыс. р.) без учёта налога на прибыль.

б) При какой ставке налога на прибыль предпринимательская деятельность будет невыгодна учителю (ставка задана в виде процента от прибыли)?

Задача №76. Расчёт величины годовых бухгалтерских и экономических издержек, экономической и бухгалтерской прибыли

Домашняя хозяйка решила открыть прачечную и рассчитывает получить годовую выручку от этого заведения, равную 120 тыс. руб.

Для того ей необходимо:

1. арендовать помещение и платить годовую арендную плату в размере 30 тыс. руб.;

2. нанять двух помощников с оплатой 20 тыс. руб. в год, труд которых будет оплачиваться из выручки;

3. купить оборудование стоимостью 60 тыс. руб.;

4. оплатить прочие расходы (инвентарь, стиральный порошок, ополаскиватели и т.д.), которые составляют 15 тыс. руб. в год.

Для покупки оборудования, срок службы которого составляет 10 лет, она решила использовать семейные сбережения. Банковский процент по депозитам равен 25%, а по кредитам – 30% годовых.

Определите:

а) величину годовых бухгалтерских и экономических издержек;

б) величину годовой бухгалтерской и экономической прибыли.

Источник

Для стимулирования сбыта своей продукции фирма ibs объявила

Бухгалтеру нужно покрасить свой дом. Для этого он может нанять начинающего маляра, который покрасит дом за 30 рабочих часов и просит за работу 1200 р.

Жена предлагает нашему бухгалтеру покрасить дом самому. Мотивирует она это тем, что бухгалтер в молодости был неплохим маляром. Он затратит на покраску 20 ч. И сэкономит семье деньги.

Бухгалтер завален работой и обычно зарабатывает 100 р. в час. Поэтому он отказывается сам красить дом, ссылаясь на экономическую целесообразность.

Кто прав и почему? Какова цена правильного выбора?

Прав бухгалтер. Он сэкономит семье деньги, если будет заниматься своей работой, которая за 20 часов принесёт ему:

20 × 100 = 2000 р.

и наймёт маляра с оплатой 1 200 р.

Цена его выбора, то есть экономия при этом составит:
2 000 – 1 200 = 800 р.

Иванов хочет отремонтировать квартиру. Он может нанять мастеров и заплатить им 15 тыс. р., а может все сделать сам, тогда ремонт будет стоить ему только 5 тыс. р. (цена материалов). Но придется взять отпуск без сохранения заработка. В день он зарабатывает 500 р. Какое максимальное число дней может потратить на ремонт Иванов, чтобы не нести убытки.

Пусть x – число дней, потраченных на ремонт.

Если Иванов будет делать ремонт сам, то недополученный заработок составит:

И ремонт обойдётся ему в сумму стоимости материалов и недополученного заработка:

Чтобы не понести убытки, эта величина должна быть не больше альтернативной стоимости ремонта Иванова — 15 000 р., то есть не больше затрат на оплату труда наёмных мастеров.

Составим и решим неравенство:

500 × х + 5 000 ≤ 15 000

Итак, Иванов может потратить на ремонт максимум 20 дней.

Петров хочет купить мебельный гарнитур. Он должен затратить на поиски дешевого и качественного варианта 7 рабочих дней, для чего намерен взять отпуск без сохранения заработка. Если он не сделает этого, то купит гарнитур на 20% дороже. В день Петров зарабатывает 1000 руб.

Какова должна быть цена гарнитура для того, чтобы рационально мыслящему Петрову было все равно – искать дешевый вариант или нет?

Пусть х – цена гарнитура в рублях.

0,2 * х – величина переплаты, в случае если Петров не возьмёт отпуск.

Если Петров возьмёт отпуск, то потери дохода составят:

7 * 1000 = 7000 р.

Рационально мыслящему Петрову будет все равно – искать дешевый вариант или нет, если величина переплаты будет равна величине потерь дохода.

Составим и решим уравнение:

Цена гарнитура должна быть равна 35 000 рублей.

Самолетом из Москвы во Владивосток можно добраться за 8 ч, но с учетом сопутствующих затрат времени можно считать, что сутки для работы или отдыха теряются. Поездка в поезде займет 9 дней. Авиабилет стоит 900 р., а железнодорожный билет 500 р.

а) Какой способ передвижения дешевле для человека, зарабатывающего 50 р. каждый рабочий день с понедельника по пятницу.

б) Если 4 из 9 дней пути на поезде приходятся на выходные, то сколько должен зарабатывать в будний день наш путешественник, чтобы ему было все равно с чисто экономической позиции — лететь в выходной день или ехать поездом?

а) Для решения данной задачи и подобных задач удобно пользоваться таблицей, в которой сравниваются альтернативные затраты двух способов путешествия.

Статьи затрат	Самолёт	Поезд
1. Недополученный заработок	50	350
2. Затраты на билет	900	500
ИТОГО	950	850

В расчёт недополученного заработка при поездке на поезде берём максимальное из 9 число будних дней, которое может истратить на поездку наш путешественник. Их будет 7. Значит, наибольшие потери дохода за 7 дней составят:

Следовательно, дешевле ехать поездом.

б) Человеку будет безразлично с чисто экономической позиции — лететь в выходной день или ехать поездом, если альтернативная стоимость полёта на самолёте будет равна альтернативной стоимости поездки на поезде.

Значит, ему должно быть всё равно либо вылететь в субботу, либо выехать в этот день поездом.

Пусть W – дневной заработок в рублях в будний день.

В случае полёта на самолёте он затратит 900 р. Потерь дохода в субботу нет.

При путешествии на поезде затраты составят:

Составим и решим уравнение:

Дневной заработок должен быть равен 80 р., тогда человеку безразлично с экономической точки зрения лететь на самолёте или ехать поездом.

Дедушка, отец и сын организовали семейный бизнес по изготовлению столов и стульев. За год отец может изготовить 50 столов или 100 стульев, дедушка — 40 столов или 100 стульев, сын 100 столов или 150 стульев. Постройте кривую производственных возможностей семьи.

Найдём оптимальную структуру производства столов и стульев. Выпуск стульев должен быть поручен тому члену семьи, чьи альтернативные издержки (альтернативная стоимость) выраженные в количестве столов минимальные.

Рассчитаем альтернативную стоимость производства одного стула для каждого члена семьи.

Для дедушки альтернативная стоимость производства одного стула:

40 / 100 = 0,4 стола ← альтернативные издержки минимальные.

Для отца альтернативная стоимость производства одного стула:

50 / 100 = 0,5 стола

Для сына альтернативная стоимость производства одного стула:

100 / 150 = 2/3 стола

Если все члены семьи будут производить только столы, они изготовят 190 столов и 0 стульев.

Допустим, они пожелают начать производство стульев. Значит дедушка, у которого альтернативная стоимость производства стульев минимальная, должен производить стулья в количестве 100 штук. Тогда производством столов будут заниматься отец и сын. Они произведут 50 + 100 = 150 штук столов. Координаты точки перелома кривой производственных возможностей: (100 стульев, 150 столов).

Если спрос по стульям не будет удовлетворён, то к их производству подключится отец. Он следующий по возрастанию значения альтернативной стоимости стульев. Вместе с дедушкой отец произведёт 200 штук стульев.

Тогда сын будет один производить столы. И произведёт их в количестве 100 штук.

Координаты ещё одной точки перелома КПВ: (200 стульев, 100 столов).

И наконец, если все участники производства будут изготавливать только стулья, будет произведено 350 стульев и 0 столов.

Изобразим КПВ на графике:

Фирма имеет кривую спроса:

Зная, что P=100 , определить изменение дохода при увеличении проданной продукции на одну единицу.

Прирост дохода при увеличении проданной продукции на одну единицу называют предельной выручкой ( MR — marginal revenue).

Предельная выручка может быть представлена как частная производная общей выручки по количеству товара.

Кроме того цена и объём связаны между собой функциональной зависимостью: Р = f(Q).

Легко заметить, что второе слагаемое в скобках есть обратное значение эластичности спроса:

Определим эластичность спроса по цене:

Таким образом, увеличение количества проданной продукции на единицу, уменьшит доход фирмы на 200 единиц.

Для стимулирования сбыта своей продукции фирма «IBS» объявила о временном снижении цен на одну из моделей компьютера с 1000 до 800 долл. В результате за следующий месяц фирма продала в два раза больше компьютеров, чем обычно.

а) Как изменилась выручка фирмы?

б) Рассчитайте коэффициент точечной эластичности (по формуле, используемой в определении) и сделайте вывод о характере спроса на данную модель компьютера.

а) Выручка фирмы рассчитывается по формуле:

Соответственно изменение выручки фирмы в процентном выражении рассчитаем по формуле:

Таким образом, выручка фирмы увеличилась на 60 %.

б) Коэффициент точечной эластичности рассчитаем по формуле, используемой в определении:

Коэффициент эластичности по абсолютной величине больше 1, следовательно спрос эластичен.

Функция задана уравнением

а) Выведите формулу эластичности этого спроса.

б) При какой цене эластичность спроса по цене составит – 0,5?

в) При какой цене в интервале цен от 200 до 300 эластичность будет максимальной по абсолютной величине?

а) Так как в условии задачи нам дана непрерывная функция, для вывода формулы эластичности этого спроса воспользуемся коэффициентом точечной эластичности.

В точке (P 0 ,Q 0 ) точечная эластичность вычисляется как

– производная функции спроса в этой точке.

б)

в) Чем больше P, тем больше эластичность по абсолютной величине. Поэтому на интервале цен от 200 до 300 она достигает максимума в точке Р=300.

Определить точечную эластичность спроса, если при снижении цены на 10 %

выручка увеличилась на 8 %.

Пусть P – первоначальная цена до её снижения, а Q – величина спроса до снижения цены.

Тогда выручка будет равна:

Из условия задачи известно, что цена снизилась на 10%, запишем это как:

А выручка увеличилась на 8%, то есть стала равна:

По-другому выручку после изменения можно записать как:

Приравняв два последних выражения, получим уравнение:

Разделим обе части уравнения на PQ

Рассчитаем точечную эластичность спроса по формуле

Так как коэффициент точечной эластичности по абсолютной величине больше единицы, следовательно спрос эластичен.

Определить точечную эластичность спроса на товар, если уменьшение цены на 5 % привело к снижению выручки на 2 %.

Пусть P – первоначальная цена до её уменьшения,

а Q – величина спроса до уменьшения цены.

Тогда выручка будет равна PQ .

Из условия задачи известно, что цена снизилась на 5%, запишем это как:

А выручка снизилась на 2%, то есть стала равна:

По-другому выручку после изменения можно записать как:

Приравняв два последних выражения, получим уравнение:

Разделим обе части уравнения на PQ

Рассчитаем точечную эластичность спроса по формуле:

Так как коэффициент точечной эластичности спроса по абсолютной величине меньше единицы, следовательно, спрос неэластичен.

Источник