Дисперсия доходности рыночного портфеля

Дисперсия (вариация) | Variance

В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

Формула

Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:

Интерпретации дисперсии

Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Пример расчета

Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.

Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.

_А = 7*0,05+15*0,2+18*0,5+24*0,2+32*0,05 = 18,75%

_Б = -24*0,05+8*0,2+20*0,5+31*0,2+57*0,05 = 19,45%

В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.

σ 2 _А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%

σ 2 _Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%

Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.

Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.

Средняя доходность акции составит 5,784%.

= (5,78+12,33-7,21+8,25+9,77)/5 = 5,784%

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.

σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%

Источник

Разница в портфеле

Что такое Разница в портфеле?

Дисперсия портфеля – это измерение риска, то есть того, как совокупная фактическая доходность набора ценных бумаг, составляющих портфель, колеблется во времени. Эта статистика отклонения портфеля рассчитывается с использованием стандартных отклонений каждой ценной бумаги в портфеле, а также корреляций каждой пары ценных бумаг в портфеле.

Ключевые моменты

• Дисперсия портфеля является мерой общего риска портфеля и представляет собой квадрат стандартного отклонения портфеля.
• Дисперсия портфеля учитывает веса и дисперсии каждого актива в портфеле, а также их ковариации.
• Более низкая корреляция между ценными бумагами в портфеле приводит к меньшей дисперсии портфеля.
• Дисперсия портфеля (и стандартное отклонение) определяют ось риска эффективной границы в современной теории портфеля (MPT).

Понимание дисперсии портфеля

Дисперсия портфеля смотрит на ковариацию или коэффициенты корреляции для ценных бумаг в портфеле. Как правило, более низкая корреляция между ценными бумагами в портфеле приводит к более низкой дисперсии портфеля.

Дисперсия портфеля рассчитывается путем умножения квадрата веса каждой ценной бумаги на ее соответствующую дисперсию и добавления удвоенного средневзвешенного веса, умноженного на ковариацию всех отдельных пар ценных бумаг.

Современная теория портфелей утверждает, что дисперсию портфеля можно уменьшить, выбрав классы активов с низкой или отрицательной корреляцией , такие как акции и облигации, где дисперсия (или стандартное отклонение) портфеля представляет собой ось x эффективной границы .

Формула и расчет дисперсии портфеля

Самым важным качеством дисперсии портфеля является то, что его стоимость представляет собой взвешенную комбинацию индивидуальных дисперсий каждого из активов, скорректированных на их ковариации. Это означает, что общая дисперсия портфеля ниже, чем простое средневзвешенное значение индивидуальных дисперсий акций в портфеле.

Формула дисперсии портфеля в портфеле с двумя активами выглядит следующим образом:

• Дисперсия портфеля = w 1 2 σ 1 2 + w 2 2 σ 2 2 + 2w 1 w 2 Cov 1,2

• w 1 = вес портфеля первого актива
• w 2 = вес портфеля второго актива
• σ 1 = стандартное отклонение первого актива
• σ 2 = стандартное отклонение второго актива
• Cov 1,2 = ковариация двух активов, которая, таким образом, может быть выражена как p (1,2) σ 1 σ 2 , где p (1,2) – коэффициент корреляции между двумя активами.

Краткая справка

Дисперсия портфеля эквивалентна квадрату стандартного отклонения портфеля.

По мере роста числа активов в портфеле члены формулы для дисперсии растут экспоненциально. Например, портфель из трех активов имеет шесть членов при расчете дисперсии, а портфель из пяти активов – 15.

Дисперсия портфеля и современная теория портфеля

Современная теория портфеля (MPT) представляет собой основу для построения инвестиционного портфеля. В основе MPT лежит идея о том, что рациональные инвесторы хотят максимизировать доходность, одновременно минимизируя риск, иногда измеряемый с помощью волатильности . Инвесторы стремятся к так называемой эффективной границе или к самому низкому уровню риска и волатильности, при котором может быть достигнута целевая доходность.

Риск портфелей MPT снижается за счет инвестирования в некоррелированные активы. Активы, которые сами по себе могут быть рискованными, могут фактически снизить общий риск портфеля за счет инвестиций, которые будут расти, когда другие инвестиции падают. Эта уменьшенная корреляция может уменьшить дисперсию теоретического портфеля.

В этом смысле доходность отдельных инвестиций менее важна, чем их общий вклад в портфель с точки зрения риска, доходности и диверсификации .

Уровень риска в портфеле часто измеряется с помощью стандартного отклонения, которое рассчитывается как квадратный корень из дисперсии. Если точки данных далеки от среднего, дисперсия высока, и общий уровень риска в портфеле также высок. Стандартное отклонение – это ключевая мера риска, используемая управляющими портфелем, финансовыми консультантами и институциональными инвесторами. Управляющие активами обычно включают стандартное отклонение в свои отчеты о производительности.

Пример отклонения портфеля

Например, предположим, что есть портфель, состоящий из двух акций. Акция A стоит 50 000 долларов и имеет стандартное отклонение 20%. Акция B стоит 100 000 долларов и имеет стандартное отклонение 10%. Корреляция между двумя акциями составляет 0,85. Учитывая это, вес портфеля Акции A составляет 33,3% и 66,7% для Акции B. Подставляя эту информацию в формулу, рассчитывается дисперсия:

• Дисперсия = (33,3% ^ 2 x 20% ^ 2) + (66,7% ^ 2 x 10% ^ 2) + (2 x 33,3% x 20% x 66,7% x 10% x 0,85) = 1,64%

Дисперсия – это не такая простая статистика для интерпретации сама по себе, поэтому большинство аналитиков вычисляют стандартное отклонение, которое является просто квадратным корнем из дисперсии. В этом примере квадратный корень из 1,64% составляет 12,81%.

Источник

Дисперсия портфеля

В общем случае дисперсия портфеля, состоящего из n инвестиционных активов, имеет вид:

В частном случае портфеля, состоящего из двух активов, дисперсия приобретает

или, с учетом формулы (3.8),

В основе современного подхода к финансовому риску лежит предположение о невозможности правильно измерить риск отдельной ценной бумаги в отрыве от других составляющих инвестиционного портфеля. Это положение легко проиллюстрировать, используя введенное понятие дисперсии портфеля как количественную меру риска.

Нашей целью будет показать на примере, как при прочих равных условиях можно добиться снижения риска инвестиционного портфеля, измеряемого его дисперсией, за счет комбинации инвестиционных активов, если корреляция последних не является строго позитивной. Предположим для простоты, что в распоряжении инвестора имеются лишь два инвестиционных актива – актив А и актив В. Для иллюстрации именно портфельного эффекта, предположим, следуя [Levy, Sarnat], что указанные выше активы имеют одинаковые распределения доходности, не имея при этом строго позитивной корреляции. Для определенности предположим, что корреляция между этими активами нулевая (ρ_АВ = 0). Предположим также, что инвестор может вложить имеющиеся у него средства либо только в актив А, либо только в В, либо 50% в А, 50% в В.

Если инвестор вкладывает все средства только в один актив, то он имеет равные шансы (то есть вероятность каждого исхода равна 0.5) как заработать 40 коп. на один вложенный рубль, так и потерять 20 коп. Это означает, что ожидаемый доход для портфеля, составленного из одного актива (А или В), составит 40•0.5 + (-20)•0.5 = 10 коп. на каждый вложенный рубль. Риск такого портфеля, измеряемый стандартным отклонением, составит [0.5(40 – 10) 2 + 0.5(-20 — 10) 2 ] 0.5 = 30 коп. на каждый вложенный рубль. Соответственно, дисперсия такого портфеля составит 900 коп 2 . Если инвестор решит распределить свои вложения поровну между активами А и В, то ожидаемый доход в соответствии с формулой (3.7) составит те же 10 коп.: Ř_p = w_A Ř_A + w_B Ř_B = 0.5•10 + 0.5•10 = 10 коп. При этом дисперсия портфеля, рассчитанная по формуле (3.10) с учетом нулевой корреляции (ρ_АВ = 0), составит:

а стандартное отклонение будет равно 21.2 коп. Таким образом, риск комбинированного портфеля существенно снизился по сравнению с портфелем, состоящим из одного актива. Этот эффект имеет место даже несмотря на то, что оба актива, использованных для комбинации, имеют идентичные показатели риска и дохода!

Полученный результат может быть достаточно просто проиллюстрирован и с позиций теории вероятностей.

Диверсификация инвестиционного портфеля

Возвращаясь к формуле (3.10), легко заметить, что чем ниже коэффициент корреляции, тем выше эффект снижения риска в результате диверсификации. Снижения общего уровня риска портфеля не будет наблюдаться только в случае строго позитивной корреляции между инвестиционными активами (ρ_АВ = 1). Столь же легко заметить, что мера риска портфеля не равна средневзвешенной сумме стандартных отклонений или дисперсий отдельных активов, входящих в портфель.

Как уже отмечалось выше, даже в условиях развитых финансовых рынков весьма трудно подобрать инвестиционные активы с негативной корреляцией, идеально подходящие для диверсификации портфеля. В лучшем случае инвестиционные активы будут иметь нулевую, либо слабо негативную корреляцию. При этом для акций обычно наблюдается позитивная корреляция, обусловленная общеэкономическими условиями. Как следствие, диверсификация позволяет снизить суммарный риск портфеля, однако не устраняет его полностью. Эмпирические исследования показывают, что обычно достаточно 15-20 случайным образом подобранных ценных бумаг, чтобы практически полностью исчерпать эффект диверсификации (соответствующая иллюстрация представлена на рисунке 3.4). Дальнейшее увеличение количества инвестиционных активов в портфеле не приводит к сколько-нибудь значимому снижению риска.

На основе анализа графической иллюстрации можно прийти к выводу о теоретической возможности разбиения суммарного риска индивидуального инвестиционного актива, как элемента портфеля, на две составляющие: диверсифицируемый (несистемный) и недиверсифицируемый (системный или рыночный) риск 4 . Первый можно определить, как риск, который может быть устранен путем диверсификации портфеля, элементом которого конкретный актив является. Внутренней связи между этой частью суммарного риска и рыночными колебаниями не существует. Системный риск путем диверсификации портфеля устранен быть не может; он обусловлен внутренней связью между колебаниями доходности конкретного актива и изменениями среднерыночной доходности.

Приведенный выше анализ портфельного риска не должен создавать иллюзию возможности «механического» подхода к диверсификации инвестиционного портфеля. Инвестиционные решения имеют достаточно сложную природу. При этом должны учитываться не только факторы риска, но и величина ожидаемого дохода, а также поведенческие мотивы.

Рис. 3.4. Зависимость риска от числа финансовых активов в портфеле

Модель оценки капитальных активов (САРМ 5 )

Ниже будет рассмотрена одна из наиболее важных в теоретическом и практическом плане проблем финансового менеджмента – проблема выработки системного подхода к оценке финансовых активов.

Формулы оценки финансовых активов как дисконтированной стоимости будущих денежных потоков, как было показано в предыдущем разделе, базируются на использовании некоторой ставки дисконтирования. Именно величина последней и определяет в значительной степени оценочную стоимость актива. Установление зависимости между уровнем риска, присущим конкретному инвестиционному активу и ожидаемой доходностью и составляет, таким образом, задачу, разрешить которую призвана рассматриваемая модель. Рассмотрение модели САРМ (читается кяпэм) именно в курсе финансового менеджмента обусловлено тем обстоятельством, что подобная модель необходима при управлении финансами предприятия как инструмент анализа при принятии инвестиционных решений, максимизирующих ожидаемый доход при заданном уровне риска. Используя модель САРМ, следует, однако, иметь в виду, что, как и любая другая модель, она является лишь приближением реальной действительности, которое лишь с определенной долей условности отражает реальную ситуацию на фондовом рынке. Современная финансовая наука наработала и другие подходы к оценке зависимости между риском и ожидаемой доходностью, в частности теорию арбитражного ценообразования С.Росса.

Основными допущениями, положенными в основу модели САРМ, являются (приводятся по [Бригхем, Гапенски] и [Levy, Sarnat]):

Основной целью каждого инвестора (который предполагается несклонным к риску) является максимизация возможного прироста своего достояния на конец планируемого периода; при этом инвестиционные решения основываются на использовании правила достижения компромисса между ожидаемым доходом и риском, измеренным при помощи среднего квадратичного отклонения

Все инвесторы могут получать и выдавать неограниченные по размерам ссуды по некоторой безрисковой процентной ставке r_f; ограничений на «короткие продажи» любых активов не существует (под «короткими продажами» понимается продажа покупателем акций, которыми он не владеет, с целью их последующего выкупа по более низкой цене)

Все инвесторы имеют одинаковые ожидания относительно дохода, дисперсии и ковариации активов. Другими словами, можно сказать, что все инвесторы находятся в равных условиях в плане доступа к информации, необходимой для принятия инвестиционных решений

Все активы абсолютно делимы и совершенно ликвидны (то есть, всегда могут быть проданы на рынке по существующей цене)

Трансакционнные издержки и налоги игнорируются

Все инвесторы принимают цену как экзогенно заданную величину (то есть, предполагают, что сделки с ценными бумагами не влияют на уровень цен последних)

Количество всех финансовых активов заранее определено и фиксировано

Инвестиционный горизонт постоянен для всех инвесторов (то есть, все инвестиционные решения принимаются в определенный момент времени, а инвестиции делаются на один и тот же период).

Перечисленные допущения являются весьма жесткими и неосуществимыми на практике. Последующий анализ применимости модели САРМ (проведенный, главным образом, в условиях американского фондового рынка) позволил несколько ослабить строгость некоторых из этих допущений. Тем не менее, вывод о степени применимости данной модели лежит в области эмпирических исследований [Бригхем, Гапенски].

Сделанные допущения позволят построить равновесную (то есть, устанавливающую равновесие между риском и ожидаемым доходом на инвестиционный актив) модель рынка капиталов. Само использование термина равновесный применительно к рынку, на котором цены непрерывно изменяются, может вызвать внутренний протест. Для разрешения кажущегося противоречия полезно использовать аналогию анализируемого явления с погоней собак за механическим зайцем на собачьих бегах [Levy, Sarnat]: «равновесие» достижимо, только если одна из собак настигнет зайца, но этого никогда не случается. Однако, осознание существования зайца (равновесие!) позволяет объяснить (и даже предсказать) поведение собак, в противном случае труднообъяснимое.

В наиболее продвинутых курсах финансового менеджмента до введения концепции коэффициента Бета (β) и линии рынка ценной бумаги принято вводить в рассмотрение понятие линии рынка капитала. Не углубляясь в теорию инвестирования, ограничимся лишь ее аналитической формулой, графической иллюстрацией (рис. 3.5) и экономической интерпретацией.

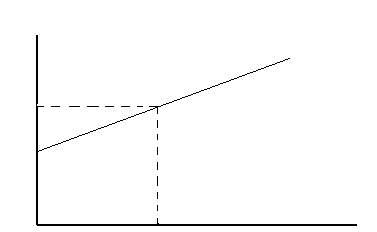
Линия рынка капитала представляет собой графическое изображение линейной зависимости между ожидаемой доходностью инвестиционного портфеля ř_p с одной стороны, и мерой портфельного риска – стандартным отклонением σ_p, с другой:

Рис. 3.5. Линия рынка капитала

Сама зависимость имеет вид:

В этом уравнении через ř_m обозначен ожидаемый доход рыночного портфеля, в то время как ожидаемая доходность ř_p относится к так называемому эффективному портфелю, обеспечивающему максимальную ожидаемую доходность при любом уровне риска или минимальный уровень риска при любой ожидаемой доходности (подробнее эффективные инвестиционные портфели будут рассмотрены ниже).

Читателю, знакомому с началами аналитической геометрии, уравнение (3.11) напомнит уравнение прямой с угловым коэффициентом. При этом наклон прямой (тангенс угла наклона) определяется отношением премии за рыночный риск (ř_m — r_f) к стандартному отклонению рыночного портфеля σ_m. Очевидно, что чем большую премию за риск ожидает инвестор, тем большую величину имеет разность (ř_m — r_f), и тем, соответственно, больше угол наклона линии рынка капитала к горизонтальной оси.

Использованные понятия безрисковой ставки, доходности и стандартного отклонения рыночного портфеля также, очевидно, нуждаются в конкретизации. В частности, в качестве безрисковой ставки в большинстве случаев принято использовать значение доходности по самым краткосрочным (чтобы минимизировать влияние процентного риска) государственным ценным бумагам. При этом следует иметь в виду, что в большинстве стран к государственным относят лишь бумаги, выпускаемые федеральным (национальным) казначейством. Понятие «рыночного портфеля» теоретически включает все ценные бумаги, присутствующие на рынке. Очевидно, что на практике приходится ограничиваться определенным набором основных компонентов рынка. В частности, может быть использован какой либо из наиболее распространенных индексов (в США это, например, Standard & Poor‘s Stock Price Index).

Логично, что следующим шагом будет переход от риска и ожидаемой доходности портфеля к риску и ожидаемой доходности отдельной ценной бумаги. При этом в рамках

модели САРМ несистемная (диверсифицируемая) составляющая общего (суммарного) риска (см. рис. 3.4) индивидуальной ценной бумаги уже не рассматривается, так как предполагается возможность его устранения путем диверсификации инвестиционного портфеля.

Концепция коэффициента Бета (β)

Как уже отмечалось выше, риск каждой отдельной ценной бумаги в инвестиционном портфеле зависит от ее корреляции с остальными составляющими портфеля. Принять во внимание коэффициенты корреляции каждого актива, входящего в портфель, особенно если этот портфель рыночный, достаточно затруднительно. Модель САРМ использует единую меру недиверсифицируемого риска отдельной ценной бумаги – коэффициент β.

В соответствии с допущениями САРМ между риском и ожидаемой доходностью на i—тую ценную бумагу в портфеле ř_i устанавливается следующее равновесное соотношение:

В соотношении (3.12) σ_im. представляет собой ковариацию между доходностью i—той ценной бумаги и доходностью рыночного портфеля. Анализ зависимости (3.12) показывает, что ожидаемый доход на индивидуальную ценную бумагу может быть представлен как сумма ставки безрисковой доходности и рыночной риск-премии (ř_m — r_f), взятой с некоторым коэффициентом. Этот коэффициент, обозначаемый β_i, учитывает степень вклада рассматриваемой i—той ценной бумаги в суммарный риск рыночного портфеля:

Таким образом, β-коэффициент служит мерой недиверсифицируемой составляющей риска, показывая, насколько рыночная риск-премия увеличивает уровень риска конкретной ценной бумаги по сравнению с безрисковым активом. Чем выше коэффициент β, тем выше уровень системного риска и, соответственно, выше уровень ожидаемой на эту ценную бумагу доходности. Другими словами, чем лучше конкретная ценная бумага ко-вариирует с рыночной доходностью, тем выше будет ожидаемый на нее доход, определяемый в процессе рыночного ценообразования на данную бумагу.

Зависимость (3.12) имеет простую геометрическую интерпретацию. Линия, выраженная уравнением (3.12), носит название линии рынка ценной бумаги (рис. 3.6). График этой линии представляет собой прямую, пересекающую вертикальную ось при β_i = 0 (для безрисковой ценной бумаги). Этой точке пересечения соответствует безрисковая ставка доходности r_f . Соответственно вклад i—той ценной бумаги в суммарный риск рыночного портфеля равен нулю. Если β_i = 1, то инвестиционный актив имеет такой же уровень риска, как и рыночный портфель. Наклон линии рынка ценной бумаги характеризует степень склонности (а, точнее, несклонности) инвесторов к риску в конкретных экономических условиях.

С течением времени положение линии рынка ценной бумаги в пространстве может меняться. Линия может перемещаться параллельно самой себе (сдвигаться) в результате изменения безрисковой ставки, например, в результате инфляции. Очевидно, что в этом

случае на соответствующую величину будет меняться и ожидаемая доходность остальных

активов рыночного портфеля. С другой стороны, линия рынка ценной бумаги может менять

свое положение в пространстве, поворачиваясь относительно безрисковой ставки r_f.

Рис. 3.6. Линия рынка ценной бумаги

Последнее может быть связано, в частности, с оптимизмом или пессимизмом инвесторов в отношении перспектив экономического развития.

Кроме того, с течением времени может меняться и сам коэффициент β, характерный для конкретной компании. Это может происходить, в частности, в результате изменения как структуры капитала фирмы, так и структуры ее активов, и, как следствие, изменения общего уровня риска ценных бумаг фирмы. Кроме того, к изменению коэффициента β могут привести внешние факторы, такие, например, как изменяющийся уровень конкуренции. Возможность изменения β-коэффициента по сравнению со значением, вычисленным по историческим данным необходимо учитывать при использовании этого коэффициента в практических целях.

Практическое использование β–коэффициента, как правило, основано на предположении, что вычисленное по историческим данным значение β (так называемое историческое, или фактическое β) достаточно хорошо отражает уровень будущего риска и, соответственно уровень ожидаемого в будущем дохода. При таком предположении пользование формулой (3.12) для расчета ожидаемого от инвестиции в конкретную ценную бумагу дохода затруднений не вызывает. При необходимости могут быть использованы различные методы коррекции для получения уточненных или фундаментальных β (подробно эти методы рассмотрены в фундаментальных курсах финансового менеджмента — см., например, [Бригхем, Гапенски, гл.6]). Пример расчета β –коэффициента по историческим данным приведен в Приложении 1 к настоящему разделу.

На практике значения коэффициента β обычно лежат в пределах от 0.5 до 2, хотя возможны и выходящие за пределы этого интервала значения. Для диверсификации инвестиционного портфеля наиболее привлекательны ценные бумаги с низкими β, хотя их число в общей структуре рынка весьма незначительно. Как отечественные ([Ковалев]), так и зарубежные ([Бригхем, Гапенски], [Levy, Sarnat] и др.) пособия по финансовому менеджменту обычно содержат примеры рассчитанных на основе исторической информации значений коэффициента β для наиболее известных компаний. В качестве суррогата рынка в условиях США чаще всего используются либо уже упоминавшийся индекс Standard & Poor‘s 500, либо индекс курсов акций Нью-Йоркской фондовой биржи (NYSE Composite Index). В российской практике также имеется опыт расчета β –коэффициентов агентством АК&М, результаты которого которые публиковались в экономической печати. При этом, используя те или иные опубликованные данные, следует иметь в виду, что даже в условиях развитых финансовых рынков рассчитанные значения показателя β зависят от ряда субъективных факторов, в частности временного периода, за который исчисляется доходность, структуры и состава суррогата, используемого в качестве «рыночного» портфеля.

В случаях, когда необходимо оценить уровень ожидаемой доходности вложения в акции компании, для которой не существует рассчитанного по историческим данным

коэффициента β, либо в проект, относящийся к виду деятельности, которым данная компания до этого не занималась, приходится использовать данные так называемых «компаний-представителей», действующий в конкретной отрасли. Подробнее процесс поиска и использования таких «компаний-представителей» описан в [Ван Хорн, гл. 15].

Достаточно часто возникает вопрос: почему в курсе финансового менеджмента столько внимания уделяется инвестициям именно в ценные бумаги, а не в какие-либо иные материальные или нематериальные активы, с чем, собственно, обычно и сталкивается предприятие прежде всего? Кроме того очевидного объяснения, что финансовый менеджмент является базовым курсом, и большинство его разделов при более глубоком изучении финансов развивается в самостоятельной курс (в частности, Корпоративных финансов или Управления инвестициями), существуют и другие причины. В частности, если принять максимизацию достояния акционеров в качестве основной цели управления финансами на предприятии, то главным объектом изучения естественным образом становятся акции фирмы – их риск и доходность, а риск любого материального актива рассматривается с точки зрения его влияния на риск акций (и доходность) [Бригхем, Гапенски]. Теоретически не только акции, но и другие активы могут стать предметом анализа при вычислении коэффициента β. Однако на практике для расчета используются практически исключительно акции, в первую очередь в силу невозможности достаточно точно оценить доходность прочих инвестиционных инструментов.

Применимость модели САРМ до сих пор является предметом широких дискуссий среди ученых-финансистов. Существует ряд исследований, как поддерживающих применение модели, так и ставящих ее под сомнение. С одной стороны, модель является фундаментальной в концептуальном плане, позволяющей на основе использования однопараметрической модели проиллюстрировать зависимость между риском и ожидаемой доходностью. С другой стороны, целый ряд эмпирических исследований не подтвердил зависимости между β –коэффициентами и историческими доходностями конкретных акций. Тем не менее, нельзя не согласиться с Ю.Бригхемом и Л.Гапенски в том, что факт отсутствия такой зависимости по результатам статистических выборок недостаточен для опровержения концепции САРМ [Бригхем, Гапенски, т.1, с 93] . Все дело в том, что модель САРМ представляет собой модель оценки ожидаемых значений доходности, и, как таковая, может быть признана логически обоснованной.

В заключение можно привести формулу для β-коэффициента портфеля:

Как и выше, w_i представляют собой веса соответствующих ценных бумаг в портфеле. В соответствии с соотношением (3.14) общий уровень риска портфеля, мерой которого служит β_p, будет повышаться либо снижаться при добавлении в портфель ценной бумаги соответственно с β 1.

Управление инвестиционным портфелем*

Приведенные выше критерии выбора инвестиций в случае одиночных активов были распространены Г.Марковицем на инвестиционные портфели. Ниже будут рассмотрены основные принципы формирования инвестиционного портфеля (детальное изложение современных подходов к формированию инвестиционного портфеля и управлению портфельными инвестициями выходит далеко за пределы базового курса финансового менеджмента и рассматривается в специальных курсах).

Очевидно, что, формируя инвестиционный портфель, инвестор будет объективно руководствоваться принципом оптимизации соотношения между риском и доходностью. Как уже отмечалось выше, это означает, что при любом заданном уровне риска инвестор будет стремиться к максимизации ожидаемой доходности, а при заданной ожидаемой доходности – стремиться к минимизации риска. Портфели, удовлетворяющие сформулированным условиям, носят название эффективных. Совокупность эффективных портфелей представляет собой выпуклую 6 кривую BCDE на Рис. 3.7 и носит название набора эффективных портфелей или границы эффективности. Все остальные портфели, находящиеся внутри фигуры ABCDEGH (помечены цифрой 2) представляют собой набор возможных портфелей (допустимое множество). Вне этой фигуры лежат портфели, не являющиеся возможными.

Источник