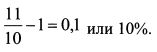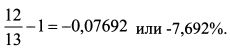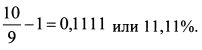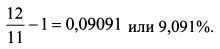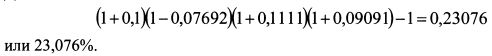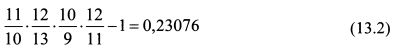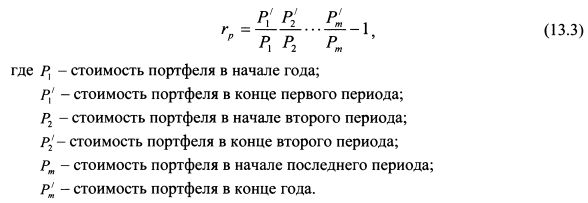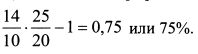Что такое среднегеометрическая доходность

Среднее геометрическое

Что такое Среднее геометрическое?

Среднее геометрическое – это среднее значение набора продуктов, расчет которого обычно используется среднее арифметическое работает с самими значениями.

Среднее геометрическое является важным инструментом для расчета эффекты начисления сложных процентов .

Ключевые моменты

• Среднее геометрическое – это средняя доходность набора значений, рассчитанная с использованием произведений условий.
• Среднее геометрическое больше всего подходит для рядов, демонстрирующих последовательную корреляцию – это особенно верно для инвестиционных портфелей.
• Большинство доходов в финансах коррелированы, включая доходность облигаций, доходность акций и премии за рыночный риск.
• Для изменчивых чисел среднее геометрическое обеспечивает гораздо более точное измерение истинной доходности за счет учета годового сложения, которое сглаживает среднее значение.

Формула для среднего геометрического

μгеометрикзнак равно
Взаимодействие с другими людьмиμгеометрическийВзаимодействие с другими людьмизнак равно[(1+р1Взаимодействие с другими людьми)(1+р2Взаимодействие с другими людьми)…(1+рпВзаимодействие с другими людьми)]1/п-1где:∙р1Взаимодействие с другими людьми…рпВзаимодействие с другими людьми доходность актива (или другогонаблюдения для усреднения) .Взаимодействие с другими людьми

Понимание среднего геометрического

Среднее геометрическое, иногда называемое совокупным годовым темпом роста или взвешенной по времени ставкой доходности , представляет собой среднюю норму доходности набора значений, рассчитанных с использованием произведений условий. Что это значит? Среднее геометрическое имеет несколько значений , и умножает их и устанавливает их в / п 1 – й мощности.

Например, вычисление среднего геометрического можно легко понять с помощью простых чисел, таких как 2 и 8. Если вы умножите 2 и 8, а затем извлечете квадратный корень (степень ½, поскольку имеется только 2 числа), ответ будет 4. Однако когда чисел много, их труднее вычислить, если не использовать калькулятор или компьютерную программу.

Краткая справка

Чем длиннее временной горизонт, тем более критичным становится сложное сложение и тем более подходящим является использование среднего геометрического.

Основное преимущество использования среднего геометрического состоит в том, что не нужно знать фактические инвестированные суммы; расчет полностью сосредоточен на самих цифрах возврата и представляет собой сравнение «яблок с яблоками» при рассмотрении двух вариантов инвестирования за более чем один период времени. Среднее геометрическое всегда будет немного меньше среднего арифметического, которое является простым средним.

Как рассчитать среднее геометрическое

Чтобы рассчитать сложные проценты с использованием среднего геометрического дохода от инвестиций, инвестору необходимо сначала рассчитать проценты в первом году, которые составляют 10 000 долларов, умноженные на 10%, или 1000 долларов. На второй год новая основная сумма составляет 11000 долларов, а 10% от 11000 долларов составляют 1100 долларов. Новая основная сумма теперь составляет 11000 долларов плюс 1100 долларов, или 12100 долларов.

На третий год новая основная сумма составляет 12 100 долларов, а 10% от 12 100 долларов составляют 1210 долларов. По прошествии 25 лет 10 000 долларов США превращаются в 108 347,06 долларов США, что на 98 347,05 долларов США больше первоначальных инвестиций. Более короткий путь состоит в том, чтобы умножить текущую основную сумму долга на единицу плюс процентную ставку, а затем поднять коэффициент до числа сложенных лет. Расчет: 10 000 долларов США

Источник

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Средняя доходность

Что такое Средняя доходность?

Средняя доходность – это простое математическое среднее ряда доходностей, генерируемых за определенный период времени. Средняя доходность рассчитывается так же, как и простое среднее значение для любого набора чисел. Числа складываются в одну сумму, а затем сумма делится на количество чисел в наборе.

Формула средней доходности

Как рассчитать средний доход

Существует несколько показателей доходности и способов их вычисления, но для средней арифметической доходности нужно взять сумму доходности и разделить ее на количество цифр доходности.

Что вам говорит средний доход?

Средняя доходность сообщает инвестору или аналитику, какова была доходность акций или ценных бумаг в прошлом или какова доходность портфеля компаний. Это не то же самое, что годовая доходность. Средняя доходность не учитывает начисление процентов.

Ключевые моменты

• Средняя доходность – это простое математическое среднее ряда доходностей.
• Это может помочь измерить прошлую доходность ценной бумаги или доходность портфеля.
• Среднее геометрическое всегда ниже средней доходности.

Пример использования средней доходности

Одним из примеров средней доходности является простое среднее арифметическое . Например, предположим, что инвестиции приносят следующую прибыль ежегодно в течение пяти полных лет: 10%, 15%, 10%, 0% и 5%. Чтобы рассчитать среднюю доходность инвестиций за этот пятилетний период, пять годовых доходов складываются и затем делятся на 5. Это дает среднегодовую доходность 8%.

Или рассмотрим Wal-Mart (NYSE: WMT). Акции Wal-Mart вернулись на 9,1% в 2014 году, потеряли 28,6% в 2015 году, выросли на 12,8% в 2016 году, выросли на 42,9% в 2017 году и потеряли 5,7% в 2018 году. Средняя доходность Wal-Mart за эти пять лет составляет 6,1% или 30,5%, разделенные на 5 лет.

Расчет прибыли от роста

Простой темп роста является функцией начальных и конечных значений или остатков. Он рассчитывается путем вычитания конечного значения из начального значения и последующего деления на начальное значение. Формула выглядит следующим образом:

Например, если вы инвестируете 10 000 долларов в компанию, а цена акций увеличивается с 50 до 100 долларов, прибыль можно рассчитать, взяв разницу между 100 и 50 долларами и разделив ее на 50 долларов. Ответ – 100 процентов, что означает, что теперь у вас есть 20 000 долларов.

Разница между средней доходностью и геометрической средней

Если смотреть на среднюю историческую доходность, среднее геометрическое является более точным расчетом. Среднее геометрическое всегда ниже средней доходности. Одним из преимуществ использования среднего геометрического является то, что не требуется знать фактические инвестированные суммы. расчет полностью сосредоточен на самих цифрах доходности и представляет собой сравнение «яблок с яблоками» при рассмотрении результатов двух или более инвестиций за более различные периоды времени.

Среднюю геометрическую доходность иногда называют взвешенной по времени ставкой доходности (TWRR), поскольку она устраняет искажающее влияние на темпы роста, создаваемое различными притоками и оттоками денег на счет с течением времени.

В качестве альтернативы, взвешенная по денежным средствам ставка доходности (MWRR) включает размер и сроки денежных потоков, поэтому она является эффективной мерой для доходности портфеля, который получил депозиты, реинвестирование дивидендов, выплату процентов или снятие средств. Доходность, взвешенная по деньгам, эквивалентна внутренней норме прибыли, где чистая приведенная стоимость равна нулю.

Ограничения использования средней доходности

Простое среднее значение доходности – это простой расчет, но он не очень точный. Для более точных расчетов доходности аналитики и инвесторы также часто используют среднее геометрическое или доходность, взвешенную по деньгам.

Источник

13.1.2. Доходность на основе средней геометрической

Случаи, когда портфель формируется за счет инвестирования какой-либо суммы только в начальный момент и на весь период времени, являются скорее исключением, чем правилом. Обычно в ходе управления портфелем средства из него как изымаются, так и дополнительно вносятся. Поэтому, рассчитывая доходность портфеля, необходимо учесть данные изменения в его стоимости, чтобы они не исказили его действительную доходность. Для этого поступают следующим образом. Разбивают весь период времени управления портфелем в рамках года на подпериоды, когда происходило добавление или изъятие средств из портфеля, и определяют доходности для каждого из этих периодов. Далее на их основе рассчитывают действительную доходность портфеля в расчете на год. Проиллюстрируем сказанное на примере.

В начале года в портфель инвестировали 10 млн. руб. Через три месяца его стоимость выросла до 11 млн. руб., и на следующий день в портфель внесли дополнительно 2 млн. руб. В конце следующего квартала стоимость портфеля составила 12 млн. руб., и из него изъяли 3 млн. руб. Еще через три месяца стоимость портфеля составила 10 млн. руб. и в него добавили 1 млн. руб. В конце года стоимость портфеля составила 12 млн. руб. Определить доходность управления портфелем.

За первый квартал стоимость портфеля выросла с 10 до 11 млн. руб. Поэтому доходность за первый квартал равна:

В начале второго квартала в портфель добавили 2 млн. руб., и стоимость его в этот момент составила 13 млн. руб. За второй квартал стоимость портфеля снизилась с 13 млн. руб. до 12 млн. руб. Доходность за второй квартал равна:

В начале третьего квартала из портфеля изъяли 3 млн. руб. и его стоимость в этот момент составила 9 млн. руб. За третий квартал стоимость портфеля выросла до 10 млн. Доходность портфеля за третий квартал оказалась равной:

В начале четвертого квартала в портфель добавили 1 млн. руб., и его стоимость составила 11 млн. руб. За четвертый квартал стоимость портфеля выросла до 12 млн. Доходность портфеля за четвертый квартал равна:

Доходность за год составила:

Для определения доходности можно не вычислять отдельно доходности для каждого периода, а записать одно уравнение, используя стоимости портфеля в начале и конце каждого временного отрезка с учетом добавлений и изъятий капитала в каждом периоде. Тогда решение задачи примет вид:

На основе алгоритма, представленного выражением (13.2), формулу определения доходности портфеля в рамках года в общем виде можно записать следующим образом:

Поскольку изъятия и поступления денег в портфель в рамках года могут происходить в любые моменты времени, то в формуле (13.3) временные периоды, на которые делится время в рамках года, также могут быть любыми.

Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.

В начале года стоимость портфеля составляла 10 млн. руб. Через 200 дней она выросла до 14 млн. руб. и в этот момент в портфель было добавлено еще 6 млн. руб. По завершении года стоимость портфеля составила 25 млн. руб. Определить доходность портфеля за истекший период.

Согласно формуле (13.3) доходность портфеля за год составила:

Выше мы определили доходность портфеля в рамках одного года. Часто эффективность управления портфелем будет оцениваться за ряд лет. Поэтому вначале следует рассчитать доходность для каждого года и после этого определить среднюю доходность в расчете на год за период управления портфелем по формуле:

Доходность за первый год составила 20%, за второй — 40%, за третий — минус 10%. Доходность портфеля в расчете на год (средняя доходность) за трехлетний период равна:

Источник